Рекурсивные функции. В результате исследований рекурсивных функций было выявлено, что они имеют непосредственную связь с алгоритмами

В результате исследований рекурсивных функций было выявлено, что они имеют непосредственную связь с алгоритмами, и можно утверждать, что любой алгоритм является рекурсией, и наоборот.

Пусть задана некоторая функция w = f(x₁, x₂, …, x _n).

Здесь f (или знак функционала) – это правило, задающее связь функции и аргумента. Функционал f может быть любым, в том числе и алгоритмом.

Тогда рекурсивными функциями называют частный случай вычислимых функций. Алгоритмы, являющиеся правилами задания функций, называют алгоритмами, сопутствующими рекурсивным функциям (АСФ).

В основе теории рекурсий лежат ограниченные множества базовых рекурсивных функций и операторов, с помощью которых, исходя из рекурсий, формируются новые функции. Если рассматривать операторы как алгоритмы, то соединение операторов позволяют получить новые алгоритмы.

Базовые рекурсивные функции могут быть трех типов:

1) Функции любого числа независимых переменных, тождественно равные нулю j_n()=0, где n – число аргументов функции (n может быть равным нулю).

Например:

АСФ в данном случае гласит: если задана функция j_n, то для любой совокупности значений аргументов значение функции равно нулю.

2) Тождественные функции любого числа независимых переменных Y_{n, i}, где n – число аргументов функции, i – номер одного из аргументов.

АСФ гласит: если задана функция Y_{n, i}, то значение функции равно значению i-го аргумента (слева направо).

Например:

Y _{3, 2}(5, 8, 0)=8

Y _{1, 1}(6)=6

Для тождественных функций:

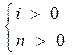
3) Функции следования одного независимого переменного l (х).

АСФ гласит: если задана функция l(х), то значением функции нужно считать число, непосредственно следующее за числом, являющимся значением аргумента.

При этом l(х)=х’ – последователь аргумента.

Например: l(5)=5’=6