Задача о выполнимости. Пусть х1, х2, , хn – множество логических переменных; – их отрицания или дополнения.

Пусть х₁, х₂, …, х_n – множество логических переменных; – их отрицания или дополнения.

if x_i = true then 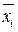= false

Ú - И; Ù - ИЛИ.

Дизъюнкция: х₁ Ú х₅ Ú 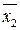Ú …

Конъюнкция: х₄ Ù х₃ Ù 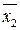Ù …

Конъюнктивная нормальная форма:

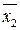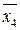E^*(x₁, …, x_n) = (x₁ Ú x₂ Ú x₃) Ù (x₁ Ú Ú ) Ù ( Ú x₄) Ù () (*)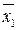

Задача о выполнимости заключается в определении, является ли булевская функция, записанная в КНФ, выполнимой.

Любая булевская функция может быть представлена в КНФ по правилу Де Моргана:

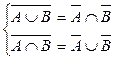
АÚ (ВÙ С)=(АÚ В)Ù (АÚ С)

Говорят, что булевская функция выполнима, если существует некоторое присваивание переменным true или false, при этом функция должна быть равна true.

Для функции (*) она будет выполнима, если ввести следующие присваивания:

(*)

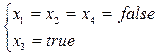
Например:

Функция

f₂(x_i)=(x₁ Ú x₂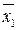)Ù ()Ù ( )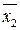

не является выполнимой, т. к. при любых x_i f₂(x_i)=false.

Теорема:

Задача о выполнимости является NP-полной.

for i=1 to N do

x_i выбор (true, false)

if E(x₁, x₂, …, x_N) then успех

else неудача

Используя преобразование задачи Р1 в Р2, можно показать, что даже ограниченный случай задачи о выполнимости является NP-полным.

К-выполнимость.

К-выполнимость означает, что любой дизъюнкт, входящий в КНФ, содержит не более К логических переменных.Минимальный случай К=3. Для булевской функции, представленной в КНФ, за полиномиальное время можно найти функцию Е^*(х₂), содержащую не более трех переменных в каждом дизъюнкте. Тогда Е выполнима, если выполнима Е^*.

E^*(x₁, x₂, …, x_n)®E^*(x_i)

Для этого используется метод уменьшения порядка дизъюнкта

(a₁ Ú a₂ Ú …Ú a_k)=(a₁ Ú a₂ Ú z) Ù (a₃ Ú a₄ Ú …Ú a_k Ú )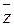

Применяя итерационный процесс разложения, можно получить Е^*.

Найти алгоритм решения Е^* проще, чем функции Е. Но при этом доказав выполнимость Е^*, докажем выполнимость исходной функции Е.

Частный случай: при К=2 функция Е входит в Р.

Примерами задач NP-класса могут послужить также задачи на графах:

1) Определение максимума клик неориентированного графа (NP-трудная задача).

2) Задача определения полного подграфа (NP-полная задача).

3) Определение вершинного покрытия мощности L для неориентированного графа (NP-полная задача).

4) Определение максимума вершинных покрытий неориентированного графа (NP-трудная задача).

5) Задача определения существования Гамильтонова цикла для графа (NP-полная задача).

6) Задача коммивояжера: определение оптимального движения по графу с единым вхождением в каждую вершину (NP-трудная задача).

7) Задача составления расписания (NP-полная задача).