Формальное определение

Пусть AP множество атомарных высказываний. моделью Крипке^[1] назовем четверку 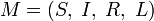состоящую из:

· конечного множества состояний ;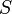

· множества начальных состояний ;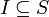

· отношения перехода 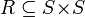, где 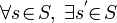такое, что ;

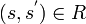· функции пометок .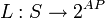

Условие накладываемое на отношение R утверждает, что каждое состояние имеет следующее. Если требуется эмулировать взаимную блокировку, в модель Крипке необходимо просто добавить ребро из состояния блокировки в себя.

Функция пометок L для каждого состояния s ∈ S определяет множество L (s) всех атомарных утверждений верных в s.

Основные понятия МЛиТА.

Теория алгоритмов, как наука, непосредственно связана с предметами математической логики и теории конечных автоматов. В Древней Греции Аристотель и его ученик Платон сформулировали основные правила логики, которые используются до нашего времени для доказательства правильности и решения логических задач.

Тео́ рия алгори́ тмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.

Математическая логика – это наука о правилах формального логического мышления.

Теория автоматов изучает модели конечных автоматов, описывающие вычислительные узлы и элементы управления ЭВМ и других технических устройств.