Изобарный процесс

Изобарными называются процессы, протекающие при постоянном давле­нии. Кривые процессов называются изобарами (рис. 4.4, 4.5).

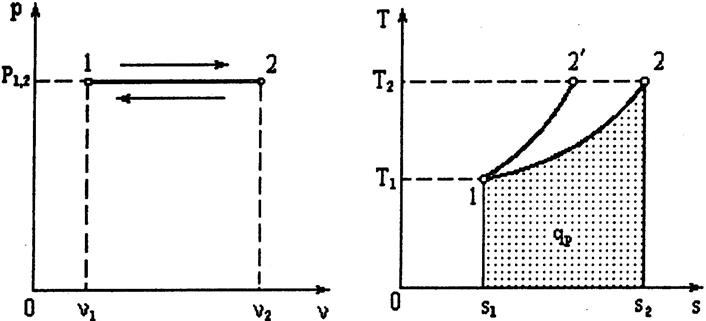
Рис. 4.4 Рис. 4.5

1. Уравнение процесса р=соnst или dp=0.

2. Соотношение параметров. Для процесса 1-2 запишем уравнение со­стояния в точках 1 и 2

;

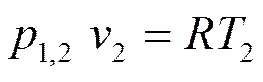
Разделив первое уравнение на второе, получим известный закон Гей-Люссака

3. Изменение внутренней энергии. Уравнение первого закона термодина­мики для изобарного процесса имеет вид

. (4.8)

Таким образом, в изобарном процессе часть теплоты, подведенной к ра­бочему телу, расходуется на изменение внутренней энергии, а оставшаяся часть идет на совершение внешней работы. Для определения долей теплоты, затрачиваемой на изменение внутренней энергии и на совершение работы, разделим уравнение (4.8) на .

Отсюда:

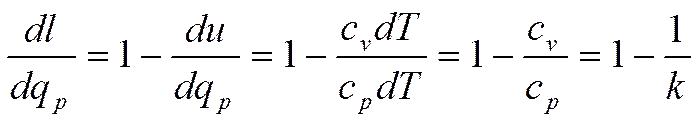
Если принять k=1, 4, что соответствует двухатомным газам, то

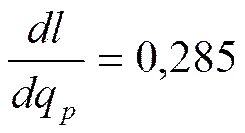, а

Следовательно, 28, 5% всей подведенной к рабочему телу теплоты в изо­барном процессе для двухатомного газа расходуется на совершение внешней работы, а 71, 5% - на изменение внутренней энергии.

Запишем уравнение первого закона термодинамики через энтальпию.

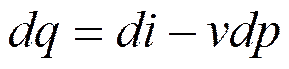
Так как dp=0, то

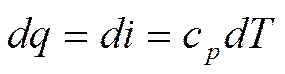(4.9)

Или при .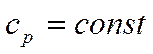

Следовательно, в изобарном процессе теплота, подведенная к рабочему телу, идет на увеличение энтальпии. Коли­чество теплоты, подведенное к рабочему телу в изобарном процессе, измеря­ется площадью под кривой процесса (рис. 4.5).

4. Работа в изобарном процессе будет , или

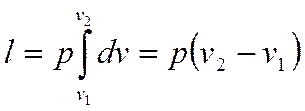
Располагаемая работа , т.к. dp=0.

5. Удельное количество теплоты определяется по уравнениям (4.8), (4.9).

6. Изменение удельной энтропии найдем из формулы (4.7), используя со­отношение параметров изобарного процесса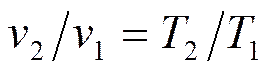

Так как по уравнению Майера , то

Подкасательная к кривой 1-2 (рис. 4.6) в любой ее точке (для точки 2 -линия АВ) в соответствующем масштабе численно равна истинной теплоем­кости .

Все изобары являются эквидистантными кривыми, имеющими при одной и той же температуре одинаковые угловые коэффициенты.

Рис. 4.6

Из уравнения Майера , следует, что . Поэтому изменение энтропии при изобарном процессе будет больше, чем при изохорном.

Из сопоставления рис. (4.3) и (4.6) следует, что изобара 1-2 (рис. 4.5) при одинаковых температурах 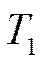, и 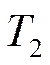, более пологая кривая, чем изохора .