Приклад виконання завдання. Розглянемо приклад виконання завдання за наступних вихідних даних: навантажувачі/добу; навантажувачів/добу; n = 2; m = 4.

Розглянемо приклад виконання завдання за наступних вихідних даних: навантажувачі / добу; 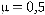навантажувачів / добу; n = 2; m = 4.

Розв’язок.

1) визначаємо параметр завантаження системи

;

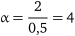2) імовірність того, що всі ремонтні пости вільні

;

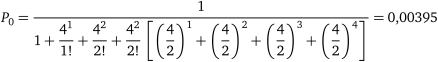3) імовірність того, що несправному навантажувачу буде відмовлено у ремонті

,

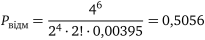Тобто, близько 50% всіх навантажувачів не будуть відремонтовані.

4) для розрахунку середньої довжини черги навантажувачів, що очікують ремонту, розрахуємо імовірності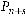

;

;

;

.

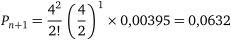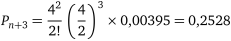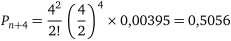5) середня довжина черги навантажувачів

;

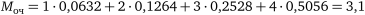6) середня тривалість очікування навантажувачем початку ремонту

доби;

7) середня кількість вільних постів ремонту

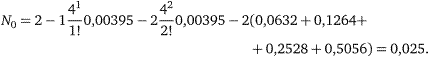
Розраховуємо ті ж самі показники при кількості постів ремонту 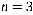, результати зводимо до таблиці 12.3.

Таблиця 12.3 — Результати розрахунку

Показник	Значення показника при кількості постів
n = 2	n = 3
	0, 5056	0, 2910
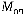
	3, 1	2, 27
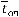
	1, 55	1, 13
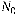
	0, 025	0, 16

Таким чином бачимо, що відсоток відремонтованих на дільниці навантажувачів збільшується приблизно на 21%, а тривалість очікування навантажувачем ремонту зменшується майже на півдоби (0, 42 доби).

Контрольні запитання

1. У чому полягають особливості функціонування системи масового обслуговування з обмеженою довжиною черги?

2. У якому випадку у системі масового обслуговування з обмеженою довжиною черги вимозі, що надходить, буде відмовлено в обслуговуванні?

3. Яким чином розраховуються імовірності всіх можливих станів системи масового обслуговування з обмеженою довжиною черги?