Стисла теоретична довідка. Транспортну мережу можна представити у вигляді графу (рисунок 13.1)

Транспортну мережу можна представити у вигляді графу (рисунок 13.1). Графом називається пара множин G = (X, A), де Х — множина вершин графа, а А — множина ребер графа.

а) б) в)

Рисунок 13.1 — Приклади графів

Граф називається орієнтованим, якщо ребра множини А орієнтовані (для ребер графа задані напрямки, що позначаються стрілками). Графи, наведені на рисунку 13.1, а, г є неорієнтованими, а граф, наведений на рисунку 13.2, б є орієнтованим. У випадку, якщо граф є орієнтованим, його ребра називають дугами.

Кожне ребро (дугу) можна записати у вигляді , де — початкова вершина, а — кінцева вершина. При цьому кажуть, що вершини та є суміжними, а ребро (дуга) є інцидентною вершинам та . Якщо початкова та кінцева вершини ребра (дуги) співпадають, таке ребро (дугу) називають петлею.

У орієнтованому графі якщо дуга виходить з вершини та заходить до вершини , вершина називається образом по відношенню до вершини , а вершина називається прообразом по відношенню до вершини .

Граф називається зваженим, якщо його ребрам (вершинам) поставлені у відповідність деякі числа, що називаються вагою ребра (вершини). Вагою ребра на графі транспортній мережі може виступати, наприклад, його довжина, вагою вершини — наявність чи потреба цієї вершини (вантажного пункту) у деякому виді вантажу.

Маршрутом у неорієнтованому графі називається послідовність ребер, у якій кожне ребро (за винятком, можливо, першого та останнього ребер) зв’язане з ребрами та 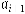своїми кінцевими вершинами. У орієнтованому графі маршрут називають шляхом. Маршрут і цикл можна задавати послідовністю вершин. Наприклад, послідовність вершин для графа на рисунку 13.1, а є маршрутом, а послідовність вершин – – – для графа на рисунку 13.1, б є шляхом. Маршрут (шлях) називається замкненим, якщо у ньому початкова та кінцева вершини співпадають.

Ланцюгом (простим шляхом) називається маршрут (шлях) у графі (орієнтованому графі), у якому жодна вершина не повторюється двічі. Циклом називається замкнений маршрут (шлях), у якому жодна з вершин, окрім першої та останньої, не повторюється двічі.

Граф називається зв’зним, якщо будь-які дві його вершини з’єднані ланцюгом (простим шляхом). Деревом називають зв’яз­ний граф без циклів (рисунок 13.1, в). Мінімальне остійне дерево графа є деревом, сума ваг ребер якого є найменшою, та яке містить на одиницю менше ребер, ніж кількість вершин графа. Мінімальне остійне дерево графа називають найкоротшою зв’язуючою мережею.

Пошук мінімального остійного дерева графа (алгоритм Краскала).

Побудувати незв’язний граф, що утворений множиною вершин вихідного графа. Упорядкувати ребра вихідного графа у порядку збільшення їх ваг. Додавати ребра з упорядкованої множини ребер до множини вершин графа таким чином, щоб при додаванні чергового ребра не утворювався цикл. Таке додавання проводити доти, поки кількість ребер дерева не стане рівним значенню, на одиницю меншому ніж кількість вершин вихідного графа.