Розв’язок. Пошук найкоротшої зв’язуючої мережі з використанням алгоритму Краскала.

Пошук найкоротшої зв’язуючої мережі з використанням алгоритму Краскала.

Згідно алгоритму знаходимо на мережі ланку з найменшою довжиною. Це ланка з (рисунок 13.4, а). Позначаємо її жирною лінією на схемі мережі.

Наступною ланкою з найменшою довжиною є ланка 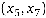з 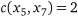. Додаємо її до будованого остійного дерева, оскільки це не призводить до виникнення циклу (рисунок 13.4, б). Наступним до рішення включаємо ланки (рисунок 13.4, в) та 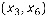(рисунок 13.4, г), що мають однакову найменшу довжину 3.

Наступним включаємо до дерева ланку довжиною 4 (рисунок 13.4, д). Наступну ланку з мінімальною довжиною 4 до дерева не включаємо, оскільки це призводить до утворення циклу . З тих самих міркувань надалі не включаємо до дерева ланку довжиною 5 (утворюється цикл – – ).

Останнім включаємо до найкоротшої зв’язуючої мережі ланку довжиною 5 і рішення припиняємо, оскільки кількість ланок у дереві дорівнює 6, що на одиницю менше, ніж кількість вершин транспортної мережі. Довжина найкоротшої зв’язуючої мережі дорівнює 18 км.

а) б)

в) г)

д) е)

Рисунок 13.4 — Знаходження найкоротшої зв’язуючої мережі

(алгоритм Краскала)

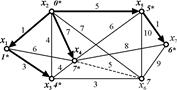
Пошук найкоротших відстаней між вершинами мережі з використанням алгоритму Дейкстри.

Знайдемо найкоротші відстані від вершини до всіх інших вершин мережі.

Крок 1. Приписуємо вершині постійну позначку (будемо позначати постійні позначки зірочкою). Іншим вершинам приписуємо тимчасові позначки (рисунок 13.5, а).

Крок 2. Переглядаємо ланки, інцидентні вершині (на рисунку 13.5, а позначені пунктиром) та для кожної суміжної вершини перераховуємо значення позначки:

ланка :

;

ланка :

;

ланка :

;

ланка :

;

ланка :

.

Крок 3. Знаходимо вершину з мінімальною тимчасовою позначкою. Це вершина з позначкою . Позначаємо її як постійну. Ланку позначаємо стрілкою (рисунок 13.5, б).

Повертаємось до кроку 2, приймаючи вершину в якості початкової. Переглядаємо ланки, інцидентні вершині , позначені тимчасовими позначками, та для кожної суміжної вершини перераховуємо значення позначки:

ланка :

;

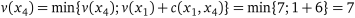а) б)

в) г)

д) е)

ж)

Рисунок 13.5 — Етапи пошуку найкоротших відстаней

на транспортній мережі (приклад)

ланка :

.

Знаходимо вершину з мінімальною тимчасовою позначкою. Це вершина з позначкою . Позначаємо її як постійну. Ланку позначаємо стрілкою (рисунок 13.5, в).

Приймаємо вершину в якості початкової. Перераховуємо тимчасові позначки суміжних з нею вершин:

ланка :

;

ланка :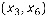

.

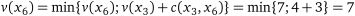Мінімальну тимчасову позначку на цьому етапі розрахунків має вершина з позначкою . Позначаємо її як постійну, ланку позначаємо стрілкою (рисунок 13.5, г).

Приймаємо вершину в якості початкової. Перераховуємо тимчасові позначки суміжних з нею вершин:

ланка :

;

ланка :

;

ланка :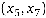

.

Знаходимо вершину з мінімальною тимчасовою позначкою. Це вершина з позначкою . Позначаємо її як постійну, ланку 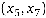позначаємо стрілкою (рисунок 13.5, д).

Приймаємо вершину в якості початкової. Перераховуємо тимчасові позначки суміжних з нею вершин:

ланка :

;

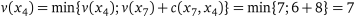ланка :

.

Мінімальну тимчасову позначку 7 мають вершини та . У цьому випадку можна обрати у якості початкової будь-яку з них. Оберемо, наприклад, вершину . Позначимо її як постійну, ланку позначимо стрілкою (рисунок 13.5, е).

Приймаючи вершину в якості початкової перераховуємо тимчасову позначку єдиної суміжної з нею вершини :

.

Остаточно позначаємо позначку вершини як постійну і на цьому припиняємо розрахунки, оскільки не залишилось жодної вершини з тимчасовою позначкою (рисунок 13.5, ж). Позначка біля вершини мережі показує найкоротшу відстань від цієї вершини до вершини . Найкоротші шляхи від вершини до всіх інших вершин мережі показані стрілками.

Контрольні запитання

1. Дайте визначення наступним поняттям: граф, орієнтований граф, зважений граф, ребро, дуга, маршрут, шлях, простий шлях, ланцюг, цикл, дерево.

2. Дайте поняття суміжності вершин та інцидентності ребер графа.

3. У якому випадку граф називають зв’язним?

4. Для чого використовують алгоритм Краскала і у чому полягає його сутність?

5. Викладіть кроки алгоритму Дейкстри для пошуку найкоротших відстаней між вершинами графа. Для яких графів він не може бути застосований?