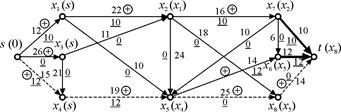
Розв’язок. Крок 2. Задаємо у мережі нульовий потік (рисунок 14.3).

Крок 2. Задаємо у мережі нульовий потік (рисунок 14.3).

Крок 3. Приписуємо витоку 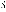позначку 0. Розглядаємо вершини, суміжні з витоком. Вершина отримує помітку 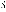, оскільки потік по дузі менше ніж її пропускна спроможність. Дуга отримує помітку «+». Аналогічним чином, помітку 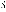отримують вершини та . Надалі, розглядаємо непомічені вершини, що суміжні вже поміченим вершинам , та . Наприклад, вершину помічаємо, розглядаючи дугу . Оскільки потік у цій дузі (він зараз дорівнює нулю) не перевищує її пропускної спроможності (22), вершина отримує помітку , а дуга — помітку «+». Приписування поміток продовжуємо, поки це можливо (рисунок 14.3).

Крок 4. В результаті приписування поміток вершина-стік отримала помітку . Це означає, що потік не є максимальним і розв’язування слід продовжити. Переходимо до кроку 5.

Крок 5. Рухаючись в зворотному порядку від вершини-стоку до вершини-витоку згідно з помітками отримуємо послідовність вершин для збільшення потоку (показаний пунктирними лініями на рисунку 14.3). Для знаходження — величини, на яку можна збільшити потік у мережі, знаходимо та . Оскільки у послідовності відсутні дуги з помітками «–», то покладаємо . Для знаходження розраховуємо для всіх дуг послідовності різницю між пропускною спроможністю дуги та потоком у ній. В результаті отримаємо:

дуга : 10 – 0 = 10;

дуга 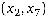: 16 – 0 = 16;

дуга : 22 – 0 = 22;

дуга : 12 – 0 = 12.

; ; ; .

Рисунок 14.3 — Початкові потоки і помітки на першій ітерації

Найменше з отриманих значень дорівнює 10, тому , а .

Збільшуємо потік у всіх дугах послідовності на 10, оскільки всі вони мають позначку «+». В результаті дуга стає насиченою (рисунок 14.4).

Подальший розрахунок згідно алгоритму показаний на рисунках 14.5 – 14.9.

; ; ; .

Рисунок 14.4 — Потоки після першої ітерації

і помітки на другій ітерації

; ; ; .

Рисунок 14.5 — Потоки після другої ітерації

і помітки на третій ітерації

; ; ; .

Рисунок 14.6 — Потоки після третьої ітерації

і помітки на четвертій ітерації

; ; ; .

Рисунок 14.7 — Потоки після четвертої ітерації

і помітки на п’ятій ітерації

; ; ; .

Рисунок 14.8 — Потоки після п’ятої ітерації

і помітки на шостій ітерації

Рисунок 14.9 – Максимальний потік і помітки на сьомій ітерації

Виконуючи приписування поміток на сьомій ітерації бачимо, що вершина-стік не отримала помітки. Це означає, що максимальний потік у мережі знайдено. Він дорівнює 36. Мінімальний розріз складають насичені дуги , та , сума пропускних спроможностей яких дорівнює максимальному потоку.

Контрольні запитання

1. Дайте поняття наступним визначенням: транспортна мережа, потік, насичена дуга, розріз.

2. Сформулюйте задачу про максимальний потік у мережі.

3. Укажіть зміст теореми Форда-Фалкерсона.

4. Як виконується приписування поміток вершинам і дугам мережі? Які значення мають помітки і за яких умов вони їх набувають?

5. Яким чином збільшується потік у транспортній мережі і за якої умови знайдений потік є максимальним?