
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стисла теоретична довідка. Теорія ігор вивчає ситуації прийняття рішень декількома взаємодіючими сторонами (їх називають гравцями)
|
|
Теорія ігор вивчає ситуації прийняття рішень декількома взаємодіючими сторонами (їх називають гравцями). Основна задача теорії ігор — пошук оптимальних стратегій, що дають гравцям найбільший середній виграш (найменший середній програш) за даних умов гри при її багаторазовому повторенні.
Стратегія — це набір правил (програма), які визначають, який із наявних ходів необхідно зробити при кожній реалізації гри. Ходом називається вибір гравцем однієї із передбачених правилами дій. Стратегії можуть бути чистими, якщо рекомендується обирати певні невипадкові ходи або змішані, в якій ходи передбачається приймати випадково.
Гра називається парною, якщо у ній беруть участь два гравці (їх позначають як А та В). Гра називається грою з нульовою сумою, якщо сумарний виграш гравців на протязі гри не змінюється та дорівнює нулю (виграш гравця А дорівнює програшу гравця В чи навпаки). Гра називається матричною, якщо у кожного з гравців А та В є обмежена кількість стратегій та умови гри задані у вигляді платіжної матриці (таблиця 16.1).
Таблиця 16.1 — Платіжна матриця гри
| Стратегії гравця А | Стратегії гравця В | |||||
| B 1 | B 2 | … | Bj | … | Bn | |
| А 1 | c 11 | c 12 | … | c 1 j | … | c 1 n |
| А 2 | c 21 | c 22 | … | c 2 j | … | c 2 n |
| ... | … | … | … | … | … | … |
| Аi | ci 1 | ci 2 | … | cij | … | cin |
| … | … | … | … | … | … | … |
| Аm |
Елементи платіжної матриці можуть бути додатними, від’ємними або рівними нулю. Якщо елемент матриці виграшів додатний то гравець В у певній ситуації сплачує стороні А суму, яка дорівнює елементу матриці. Якщо елемент матриці від’ємний, то гравець А сплачує стороні В суму, яка дорівнює абсолютному значенню елемента матриці. Якщо елемент матриці дорівнює нулю, ніякої сплати не відбувається.
Розв’язання гри полягає у знаходженні оптимальних стратегій гравців
 ;
;  ; (16.1)
; (16.1)
де p 1, p 2,..., pm — імовірності вибору гравцем А його чистих стратегій A 1... Am;
q 1, q 2,..., qn — імовірності вибору гравцем В його чистих стратегій B 1... Bn.
Дотримання гравцями оптимальних стратегій дає можливість одержати кожному з них максимальний середній виграш (мінімальний середній програш), що називається ціною гри.
Гра називається такою, що має сідлову точку, якщо її нижня ціна  дорівнює верхній ціні
дорівнює верхній ціні 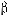 :
:
 ;
;  ;
;  . (16.2)
. (16.2)
У випадку, коли гра має сідлову точку кажуть, що гра має рішення в чистих стратегіях.
При рішенні гри слід керуватись такою послідовністю дій:
1) знайти верхню та нижню ціну гри та перевірити наявність у гри сідлової точки та рішення у чистих стратегіях;
2) за відсутності у гри сідлової точки спробувати спростити гру, шляхом виключення з платіжної матриці домінуючих (заздалегідь невигідних) та дублюючих стратегій;
3) після спрощення платіжної матриці гри її рішення проводять одним з методів, з огляду на кількість стратегій кожного гравця: гра 2´ 2 вирішується аналітичним методом; гра 2´ m чи n ´ 2 — графоаналітичним методом, гра m ´ n — методом лінійного програмування чи методом ітерацій.