Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язок. Спочатку перевіримо, чи є у гри сідлова точка (рішення в чистих стратегіях)
|
|
Спочатку перевіримо, чи є у гри сідлова точка (рішення в чистих стратегіях). Для цього знаходимо нижню ціну гри 
та верхню ціну гри 
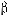(таблиця 17.4).
Таблиця 17.4 — Перевірка наявності сідлової точки
| В 1 | В 2 | В 3 | В 4 | 
| 
| |
| А 1 | ||||||
| А 2 | –2 | –1 | –2 | |||
|  ; 
| |||||
|
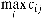
Так як нижня ціна гри не дорівнює верхній, тобто , то робимо висновок, що гра не має сідлової точки та рішення у чистих стратегіях.
Спробуємо спростити платіжну матрицю гри.
Розглянемо гру з позицій гравця В. Порівнюючи його активні стратегії В 2 та В 4 помічаємо, що стратегія В 2 для гравця В є заздалегідь невигідною, оскільки при будь-якому ході гравця А він програє більше, використовуючи активну стратегію В 2 ніж використовуючи активну стратегію В 4. Як кажуть, стратегія В 4 домінує стратегію В 2. Таким чином, стратегію В 2 з гри можна виключити, в результаті отримуємо гру з платіжною матрицею 2´ 3 (таблиця 17.5).
Таблиця 17.5 — Спрощена платіжна матриця
| В 1 | В 3 | В 4 | |
| А 1 | |||
| А 2 | –2 | –1 |
Складаємо функціональні рівняння середньоочікуваних виграшів гравця А за формулою (17.1):
;
;
.
За складеними рівняннями у системі координат 
будуємо відповідні графіки рівнянь 
(рисунок 17.1).
Рисунок 17.1 — Графіки рівнянь 
Будуємо графік функції 
. Він охоплює нижню границю побудованих прямих та утворює контур ABCD (на рисунку 17.1 він показаний жирними лініями).
Екстремальна (максимальна) точка контуру — точка С. У ній перетинаються прямі 
та 
. Отже, отримуємо гру 2´ 2, у якій з боку гравця В маємо дві активні стратегії — В 3 та В 4 (таблиця 17.6).
Таблиця 17.6 — Гра 2´ 2
| В 3 | В 4 | |
| А 1 | ||
| А 2 | –1 |
Оптимальні змішані стратегії гравців знаходимо за формулами (16.3):
; 
;
; 
;
.
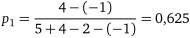Тобто,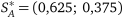 
, 
, 
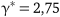. Автотранспортному підприємству слід з імовірністю 0, 25 (25 днів зі 100) виділяти рухомий склад за третім варіантом, та з імовірністю 0, 75 (75 днів зі 100) — за четвертим варіантом. При цьому рухомий склад 62, 5% днів відпрацює на першому маршруті та 37, 5% днів — на другому маршруті, а підприємство буде одержувати середній щоденний прибуток 2, 75 у.г.о.
Контрольні запитання
1. Як виконується спрощення платіжної матриці гри? Поясніть принцип домінування стратегій.
2. Поясніть порядок рішення ігор 2´ n та m ´ 2 графоаналітичним методом.
3. У чому полягає відмінність у графоаналітичному розв’язуванні ігор 2´ n у порівнянні з іграми m ´ 2?
4. Викладіть зміст теореми про кількість активних стратегій гравців у парних матричних іграх з платіжною матрицею довілього розміру.