
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язок. Попередній аналіз платіжної матриці гри показує, що гра не має сідлової точки:
|
|
Попередній аналіз платіжної матриці гри показує, що гра не має сідлової точки:
 ;
;
 .
.
 .
.
Серед елементів платіжної матриці є від’ємні, найменше з яких дорівнює  . Отже, перехід до платіжної матриці з додатними елементами можна, призначивши
. Отже, перехід до платіжної матриці з додатними елементами можна, призначивши 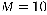 та додавши це значення до всіх її елементів (таблиця 18.3).
та додавши це значення до всіх її елементів (таблиця 18.3).
Таблиця 18.3 — Перетворена платіжна матриця гри
| В 1 | В 2 | В 3 | |
| А 1 | |||
| А 2 | |||
| А 3 |
На підставі цієї перетвореної платіжної матриці формулюємо дві двоїсті задачі лінійного програмування:
для стратегій гравця А

 ; ;
 ; ;
 . .
 ( (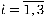 ) )
| для стратегій гравця В
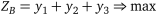
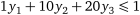 ; ;
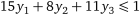 ; ;
 . .
 ( ( ) )
|
Вирішуючи ці дві задачі отримаємо:
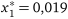 ;
;  ;
;  ;
;  ;
;
 ;
; 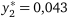 ;
;  ;
;  .
.
Розраховуємо ціну гри і компоненти оптимальних змішаних стратегій гравців для перетвореної (таблиця 18.3) платіжної матриці:
 ;
;
 ;
;
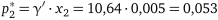 ;
;
 ;
;
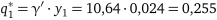 ;
;
 ;
;
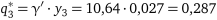 .
.
Дійсна ціна гри для вихідної платіжної матриці
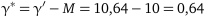 .
.
Оптимальною стратегією АТП буде  , тобто слід у 20, 2% днів планового періоду виділяти для перевезень автомобілі першого типу, у 5, 3% днів — автомобілі другого типу і у 75, 5% днів — автомобілі третього типу. При цьому автомобілі будуть 25, 5% днів перевозити перший вид вантажу, 45, 8% днів — другий вид вантажу і 28, 7% днів — третій вид вантажу. Це економічно вигідно АТП, оскільки воно буде в середньому отримувати щодня 0, 64 у. г. о. прибутку.
, тобто слід у 20, 2% днів планового періоду виділяти для перевезень автомобілі першого типу, у 5, 3% днів — автомобілі другого типу і у 75, 5% днів — автомобілі третього типу. При цьому автомобілі будуть 25, 5% днів перевозити перший вид вантажу, 45, 8% днів — другий вид вантажу і 28, 7% днів — третій вид вантажу. Це економічно вигідно АТП, оскільки воно буде в середньому отримувати щодня 0, 64 у. г. о. прибутку.
Контрольні запитання
1. При якому розмірі платіжної матриці гри для її рішення можна застосувати метод лінійного програмування?
2. Якими повинні бути елементи платіжної матриці гри для її рішення методом лінійного програмування?
3. Запишіть умови пари двоїстих задач лінійного програмування для знаходження компонентів оптимальних змішаних стратегій гравців при рішенні гри методом лінійного програмування.
4. Як, знаючи рішення пари двоїстих задач лінійного програмування, знайти імовірності використання гравцями активних стратегій у грі?
5. Як знайти дійсну ціну гри, якщо для вихідної платіжної матриці застосовувалось перетворення?