Розв’язок. У таблиці 19.2 наведені перші 15 кроків ітераційного процесу

У таблиці 19.2 наведені перші 15 кроків ітераційного процесу. Рішення починаємо з того, що гравець А обирає будь-яку свою активну стратегію (у нашому прикладі стратегію А ₃).

Нижче наведені пояснення до ітераційної таблиці.

1. У першому стовпчику зазначений номер розігруваної партії (пари виборів) 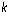, у другому — номер і вибраної у даній партії стратегії гравця А.

2. У наступних трьох стовпчиках записують накопичений виграш за перші 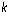партій при тих стратегіях, які застосовували гравці у попередніх партіях та при стратегіях B ₁ , B ₂ , B ₃гравця В у даній партії. Результат одержується додаванням елементів відповідного рядка платіжної матриці до значень попереднього рядка розрахункової таблиці.

3. Серед цих накопичених виграшів знаходять мінімальний (у таблиці 19.2 такий виграш позначено зірочкою). Якщо мінімальних виграшів декілька, позначаються всі. Позначене число визначає відповідний вибір гравця В у даній партії — він обирає ту стратегію, яка відповідає позначеному мінімальному виграшу (якщо їх декілька, вибирається будь-яке). Таким чином, визначається номер оптимальної (у даній партії) стратегії гравця В. Номер цієї стратегії записується у наступному стовпчику.

4. У наступних трьох стовпчиках фіксується накопичений виграш за 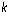партій, відповідно, при стратегіях A ₁, A ₂ , A ₃ гравця А (визначається додаванням елементів відповідного стовпчика платіжної матриці до значень попереднього рядка розрахункової таблиці). З цих значень у таблиці 19.2 позначено зірочкою максимальне — воно визначає вибір стратегії сторони А у наступній партії (рядком нижче).

5. В останніх трьох стовпчиках таблиці 19.2 записують: 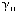— нижню оцінку ціни гри, яка дорівнює накопиченому виграшу гравця А, поділеному на кількість розіграних партій 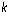; 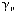— верхню оцінку ціни гри, яка дорівнює накопиченому виграшу гравця В, поділеному на 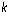; 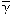— середнє арифметичне між цими двома оцінками.

Таблиця 19.2 — Розрахункова таблиця

Номер партії	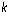Стратегія гравця А	Накопичений виграш гравця А при стратегіях гравця В	Стратегія гравця В	Накопичений виграш гравця В при стратегіях гравця А	Ціна гри
В 1	В 2	В 3	А 1	А 2	А 3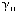
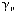
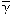
				–2*		10*		–2	–2
		–6*					6*		–3
		–1*	–1*				4*		–0, 33	1, 33	0, 5
			–3*					3*	–0, 75	0, 75	0
			–2*					4*	–0, 4	0, 8	0, 2
			–1*				–2	5*	–0, 17	0, 71	0, 27
			0*				–4	6*		0, 86	0, 43
			1*				–6	7*	0, 13	0, 88	0, 51
				0*		11*	–5			1, 22	0, 61
			2*			11*	–3		0, 2	1, 1	0, 65
		1*						7*	0, 09	0, 64	0, 37
			3*					8*	0, 25	0, 67	0, 46
			4*				–2	9*	0, 31	0, 69	0, 5
			5*				–4	10*	0, 36	0, 71	0, 54
			6*				–6	11*	0, 4	0, 73	0, 57

Для знаходження наближеного рішення гри необхідно підрахувати частоту використання активних стратегій гравців за виконану кількість кроків ітераційного процесу .

Гравець А використав за 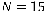партій стратегію А ₁ 3 рази (), стратегію А ₂ — 2 рази (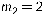), стратегію А ₃ — 10 разів ().

Гравець В використав за 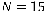партій стратегію В ₁ 2 рази (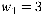), стратегію В ₂ — 11 разів (), стратегію В ₃ — 2 рази ().

Таким чином, наближені значення компонентів оптимальних змішаних стратегій гравців складуть:

гравця А:

; ; ;

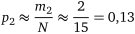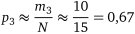гравця В:

; ; .

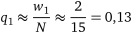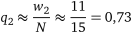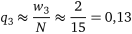Наближене значення ціни гри (значення 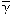у останньому рядку розрахункової таблиці) .

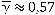Для порівняння наведемо точне рішення гри, отримане у практичному занятті 18:

; ; .

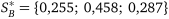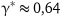Контрольні запитання

1. Для рішення яких ігор призначений наближений ітераційний метод Брауна-Робінсон? У чому полягає його сутність?

2. З яких стовпчиків складається розрахункова таблиця і як заповнюються її рядки?

3. Укажіть переваги та недоліки методу Брауна-Робінсон.