
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклад виконання завдання. Розглянемо приклад виконання завдання за таких вихідних даних: n = 5; автомобіля/добу; автомобіль/добу; доби.
|
|
Розглянемо приклад виконання завдання за таких вихідних даних: n = 5;  автомобіля / добу;
автомобіля / добу; 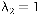 автомобіль / добу;
автомобіль / добу;  доби.
доби.
Розв’язок.
1. Визначаємо інтенсивність обслуговування
 автомобілів / добу.
автомобілів / добу.
2. Визначаємо відносні параметри завантаження системи
 ;
;  .
.
3. Подальші розрахунки зводимо до таблиці 7.3.
Таблиця 7.3 — Розрахунок СМО з пріоритетами
| k | 
| 
| 
| 
|
| 1, 00 | 0, 0045 | 0, 0225 | ||
| 3, 75 | 0, 0169 | 0, 0676 | ||
| 7, 03 | 0, 0316 | 0, 0948 | ||
| 8, 79 | 0, 0396 | 0, 0792 | ||
| 8, 24 | 0, 0371 | 0, 0371 | ||
| 6, 18 | 0, 0278 | |||
| 34, 99 | 0, 301 |
4. Розраховуємо коефіцієнти  та
та  :
:
 (сума значень у третьому стовпчику таблиці 7.3);
(сума значень у третьому стовпчику таблиці 7.3);
 .
.
5. Імовірність того, що всі ремонтні бокси вільні
 .
.
6. Імовірність відмови в обслуговуванні автомобілям приватних осіб складає
 .
.
7. Середня кількість вільних боксів
 .
.
8. Середня тривалість очікування обслуговування автомобілями власного парку
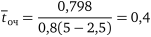 доби.
доби.
9. Середня довжина черги автомобілів власного парку
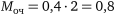 автомобіля.
автомобіля.
Контрольні запитання
1. Поясніть особливості функціонування системи масового обслуговування з пріоритетами.
2. Які види пріоритетів існують в системах масового обслуговування?
3. У чому полягає відмінність при обслуговуванні вимог першого та другого типів.
4. Наведіть послідовність розрахунку показників функціонування системи масового обслуговування з пріоритетами.
САМОСТІЙНА РОБОТА №8
ТРАНСПОРТНА ЗАДАЧА НА МЕРЕЖІ
Мета заняття: вивчення методу рішення транспортної задачі лінійного програмування на мережі методом потенціалів.
Стисла теоретична довідка
У мережевій постановці транспортної задачі постачальники з запасами, споживачі з потребами та відстані між ними задані безпосередньо на транспортній мережі.
Транспортна мережа складається з окремих елементів. Транспортні пункти називаються вершинами мережі, а дуги, що з’єднують їх називаються ланками мережі. На схемах зазвичай вершини, що відповідають постачальникам, позначають квадратиками, а вершини, що відповідають споживачам, позначають кружечками. Всередині квадратиків та кружечків записують відповідний запас вантажу чи потребу у ньому. Поруч з ланками мережі записують вартість транспортування одиниці вантажу по даній ланці. Ланки, по яких спрямовується вантажопотік, позначаються подвійними лініями зі стрілками, біля яких у кружечку записується величина вантажопотоку.
У загальному вигляді транспортна задача на мережі формулюється наступним чином.
Задана транспортна мережа S. Кожній ланці цієї мережі  поставлено у відповідність невід’ємне число
поставлено у відповідність невід’ємне число  , що розглядається як вартість переміщення по цій ланці одиниці вантажу (зокрема, довжина ланки). У деяких вершинах цієї мережі розташовані постачальники однорідного продукту (джерела з додатними інтенсивностями). У деяких вершинах мережі розташовані споживачі (джерела з від’ємними інтенсивностями). У загальному випадку кожній вершині
, що розглядається як вартість переміщення по цій ланці одиниці вантажу (зокрема, довжина ланки). У деяких вершинах цієї мережі розташовані постачальники однорідного продукту (джерела з додатними інтенсивностями). У деяких вершинах мережі розташовані споживачі (джерела з від’ємними інтенсивностями). У загальному випадку кожній вершині  задана інтенсивність
задана інтенсивність  , причому сума інтенсивностей по всім вершинам мережі дорівнює нулю, що означає загальний баланс відправлень та отримань.
, причому сума інтенсивностей по всім вершинам мережі дорівнює нулю, що означає загальний баланс відправлень та отримань.
Кожною ланкою мережі між вершинами  та
та  може прямувати невід’ємний потік продукту (вантажопотік)
може прямувати невід’ємний потік продукту (вантажопотік)  . Потоки на ланках заздалегідь невідомі, але вони зв’язані у кожній вершині умовою балансу: загальна кількість вантажу, що прибуває до вершини у сумі з інтенсивністю цієї вершини дорівнює загальній кількості вантажу, що відправляється з цієї вершини. Умова балансу у поєднанні з вимогою невід’ємності вантажопотоків визначає множину допустимих планів задачі.
. Потоки на ланках заздалегідь невідомі, але вони зв’язані у кожній вершині умовою балансу: загальна кількість вантажу, що прибуває до вершини у сумі з інтенсивністю цієї вершини дорівнює загальній кількості вантажу, що відправляється з цієї вершини. Умова балансу у поєднанні з вимогою невід’ємності вантажопотоків визначає множину допустимих планів задачі.
Необхідно знайти такий допустимий план перевезень  , щоб значення цільової функції
, щоб значення цільової функції  (транспортних витрат) було найменшим.
(транспортних витрат) було найменшим.
Транспортна задача у мережевій постановці може бути закритого та відкритого типів. Задача називається задачею закритого типу, якщо на мережі виконується умова балансу між загальною наявністю продукту та його загальним споживанням, тобто
 .
.
У задачах відкритого типу умова балансу не виконується, тобто
 чи
чи  .
.
Задачі відкритого типу зводяться до задач закритого типу шляхом введення фіктивного постачальника чи споживача. Наприклад, у випадку, якщо  , то передбачається, що до кожної вершини-відправника
, то передбачається, що до кожної вершини-відправника  підходить ланка
підходить ланка  , що зв’язує її з однією для всіх вершин-відправників фіктивною вершиною-споживачем
, що зв’язує її з однією для всіх вершин-відправників фіктивною вершиною-споживачем 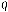 з потребою у вантажі
з потребою у вантажі 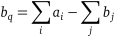 . Довжина ланки
. Довжина ланки  в напрямку від вершини
в напрямку від вершини  до вершини
до вершини 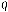 приймається рівною нулю, а у зворотному напрямку — достатньо великому додатному числу
приймається рівною нулю, а у зворотному напрямку — достатньо великому додатному числу  .
.
Таким чином, в процесі рішення транспортної задачі на мережі визначаються не розміри поставок від постачальників до споживачів, а вантажопотоки на ланках транспортної мережі, які будуть виникати при реалізації оптимального плану перевезень.
Для рішення транспортної задачі на мережі розроблено декілька методів, зокрема метод потенціалів.
Системою потенціалів називають систему чисел, що ставлять у відповідність кожній вершині мережі. Потенціал і -ї вершини позначається як  та записується поруч з вершиною. Сутність методу полягає у побудові такої системи вантажопотоків, щоб виконувалась умова оптимальності: для кожної ланки абсолютна величина різниці потенціалів вершин
та записується поруч з вершиною. Сутність методу полягає у побудові такої системи вантажопотоків, щоб виконувалась умова оптимальності: для кожної ланки абсолютна величина різниці потенціалів вершин  та
та  , які вона з’єднує, не повинна перевищувати (для ланок з вантажопотоком повинна строго дорівнювати) вартості перевезень між ними:
, які вона з’єднує, не повинна перевищувати (для ланок з вантажопотоком повинна строго дорівнювати) вартості перевезень між ними:
 при
при 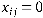 ;
;
 при
при  .
.
Рішення транспортної задачі на мережі методом потенціалів полягає у виконанні наступних кроків.
Крок 1. Знаходження початкового допустимого базисного плану постачань.
Початковий план постачань складається довільним чином з дотриманням наступних вимог:
а) всі запаси постачальників повинні бути розподілені, а всі потреби споживачів задоволені;
б) до кожної вершини-споживача повинно підходити, а з кожної вершини-постачальника відходити не менше однієї ланки з вантажопотоком;
в) кількість ланок з вантажопотоком повинна бути на одиницю менше загальної кількості постачальників та споживачів на мережі;
г) ланки з вантажопотоком не повинні утворювати замкнений контур.
Крок 2 .Визначення потенціалів вершин мережі.
Потенціали вершин визначають наступним чином. Будь-якій з вершин  присвоюють будь-яке початкове значення потенціалу
присвоюють будь-яке початкове значення потенціалу  . Далі знаходять ланку з вантажопотоком (завантажену ланку), що з’єднує цю вершину з деякою вершиною
. Далі знаходять ланку з вантажопотоком (завантажену ланку), що з’єднує цю вершину з деякою вершиною  . Величина потенціалу
. Величина потенціалу  вершини
вершини  визначається за формулою
визначається за формулою
 .
.
У наведеній вище формулі приймають знак «+» у випадку, якщо вантажопотік прямує у напрямку з вершини  до вершини
до вершини  , і знак «–», якщо вантажопотік прямує у напрямку з вершини
, і знак «–», якщо вантажопотік прямує у напрямку з вершини  до вершини
до вершини  .
.
Переглядаючи таким чином послідовно всі вершини мережі визначають їх потенціали.
Крок 3 .Перевірка умови оптимальності для всіх ланок без вантажопотоку (вільних ланок).
Для всіх вільних ланок розраховують величину оцінок  за формулою
за формулою
 .
.
Якщо серед розрахованих таким чином оцінок всі  , то при розв’язуванні транспортної задачі на мінімум вартості перевезень даний план є оптимальним.
, то при розв’язуванні транспортної задачі на мінімум вартості перевезень даний план є оптимальним.
Якщо ж наявне хоча б одне від’ємне значення оцінки, то даний план перевезень не є оптимальним та можна перейти до іншого плану, для якого транспортні витрати будуть менше. Це можна зробити, направивши вантажопотік ланкою, для якої  (крок 4).
(крок 4).
Крок 4. Покращення плану перевезень.
Для переходу до нового, поліпшеного плану перевезень виконують наступні дії:
а) вибирають ланку з найбільшим за абсолютною величиною значенням від’ємної оцінки  . Ця ланка називається перспективною ланкою;
. Ця ланка називається перспективною ланкою;
б) цією ланкою направляють вантажопотік від вершини з меншим значенням потенціалу до вершини з більшим значенням потенціалу (перспективний вантажопотік);
в) для визначення величини перспективного вантажопотоку будують замкнений контур, що складається з перспективної ланки та завантажених ланок мережі. У цьому контурі переглядаються вантажопотоки, напрямок яких є протилежним напрямку перспективного вантажопотоку. З цих вантажопотоків обирається найменший за величиною, значення якого і присвоюють перспективному вантажопотоку;
г) у розглядуваному замкненому контурі виконують перерозподіл вантажопотоків за наступним правилом: попередньо знайдена величина перспективного вантажопотоку додається до всіх величин вантажопотоків, напрямок яких співпадає з перспективним, та віднімається від всіх величин вантажопотоків, напрямок яких є протилежним перспективному.
При виконанні перерозподілу вантажопотоків необхідно слідкувати за тим, щоб кількість завантажених ланок в результаті не змінювалась. У необхідних випадках слід залишати у плані поставок фіктивні вантажопотоки (завантажені ланки з нульовим значенням вантажопотоку).
Після перерозподілу вантажопотоків повертаються до кроку 2.
Зміст роботи та вихідні дані до її виконання
Найти оптимальний план перевезень однорідного вантажу за критерієм мінімуму обсягу транспортної роботи у тонно-кілометрах. Варіанти схем транспортної мережі (довжина ланок задана у кілометрах) наведені на рисунках 8.1–8.4. Дані про наявність вантажу у постачальників та варіант схеми транспортної мережі наведені у таблиці 8.1, про потреби у вантажі споживачів — у таблиці 8.2.

Рисунок 8.1 — Схема транспортної мережі (варіант 1)

Рисунок 8.2 — Схема транспортної мережі (варіант 2)
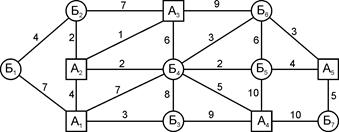
Рисунок 8.3 — Схема транспортної мережі (варіант 3)

Рисунок 8.4 — Схема транспортної мережі (варіант 4)
Таблиця 8.1 — Варіант схеми транспортної мережі та наявність вантажу у постачальників
| Варіанти | Наявність вантажу у постачальників, т | |||||
| завдання | схеми | А1 | А2 | А3 | А4 | А5 |
Продовження таблиці 8.1.
| Варіанти | Наявність вантажу у постачальників, т | |||||
| завдання | схеми | А1 | А2 | А3 | А4 | А5 |
Таблиця 8.2 — Потреби у вантажі споживачів
| Варіант | Потреба у вантажі одержувачів, т | |||||||||||||||
| Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | ||||||||||
Продовження таблиці 8.2.
| Варіант | Потреба у вантажі одержувачів, т | ||||||||||||||
| Б1 | Б2 | Б3 | Б4 | Б5 | Б6 | Б7 | |||||||||