Стисла теоретична довідка. Прийняття рішень в умовах невизначеності характеризується тим, що дії однієї з конфліктуючих сторін залежать не від свідомо діючого об’єкта

Прийняття рішень в умовах невизначеності характеризується тим, що дії однієї з конфліктуючих сторін залежать не від свідомо діючого об’єкта, а набувають властивостей невизначеності (об’єктивної дійсності). Такого супротивника у грі прийнято називати природою (П). Дії природи відрізняються від дій свідомого гравця тим, що природа, на відміну від гравця, який кожним ходом намагається завдати супротивнику найбільшої шкоди, діє невизначено, зокрема, можливо, на користь супротивнику.

Для прийняття рішень у таких іграх застосовують різноманітні критерії, в залежності від наявності інформації про стан природи. Нижче наведені деякі класичні критерії прийняття рішень у грі з природою.

1. Максимінний критерій Вальда.

Згідно з цим критерієм вибирається така стратегія гравця А, яка гарантує при будь-яких умовах виграш не менший ніж максимін відповідної платіжної матриці гри

. (20.1)

Якщо керуватись цим критерієм, то необхідно завжди орієнтуватись на найгірший результат у грі і обирати таку стратегію, при якій виграш у найгірших умовах буде максимальним.

2. Мінімаксний критерій ризику Севіджа.

У цьому випадку при виборі оптимальної стратегії слід орієнтуватися не на виграш, а на ризик. Ризиком гравця А при виборі деякої стратегії A_i в умовах природи П_j називається різниця між максимальним виграшем, що можна одержати, якщо знати наміриприроди, і виграшем, який отримає гравець А в тих же умовах, застосовуючи стратегію A_i. Якщо б гравець А знав заздалегідь майбутній стан природи П, то він обрав би стратегію, якій відповідає максимальний елемент у даному стовпчику, тобто . Тоді величина ризику за визначенням дорівнює .

Матриця ризиків будується таким чином:

1) визначається для кожного стану природи (стовпчика) найбільший елемент ;

2) елемент матриці ризиків одержують відніманням відповідного елементу платіжної матриці з максимального елемента даного стовпчика.

Критерій Севіджа рекомендує в умовах невизначеності обирати стратегію, що забезпечує мінімальне значення максимального ризику

. (20.2)

3. Критерій песимізму-оптимізму Гурвіца.

Згідно з цим критерієм для кожної активної стратегії гравця визначають лінійну комбінацію мінімального та максимального виграшу і обирають ту стратегію, для котрої ця величина буде найбільшою.

Критерій Гурвіца записується у вигляді

. (20.3)

де — коефіцієнт, що характеризує ступінь оптимізму ().

Коефіцієнт вибирається з суб’єктивних міркувань в залежності від ступеня відповідальності: чим більше наслідки помилкових рішень, тим більше бажання застрахуватись від ризику, отже, тим ближче до нуля вибирається .

При критерій Гурвіца перетворюється у максимінний критерій Вальда.

При критерій Гурвіца є критерієм «крайнього» оптимізму, який рекомендує обирати ту стратегію, що забезпечує у найкращих умовах максимальний виграш.

4. Критерій Баєса–Лапласа.

Вибираючи цей критерій, відходять від умов повної невизначеності, вважаючи, що можливим станам природи можна надати певну імовірність їх появи. Визначивши математичне очікування виграшу для повного розв’язання, вибирають те, котре забезпечує найбільше значення виграшу

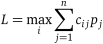, (20.4)

де — ймовірність появи j -го стану природи.

Принцип Байєса–Лапласа можна застосовувати, якщо досліджувані стани природи та рішення, які приймаються, багаторазово повторюються. Тоді, наприклад, статистичними методами, базуючись на частотах появи окремих станів природи у минулому, можна оцінити імовірність їх появи у майбутньому. При одиничних рішеннях, які не повторюються, принцип Байєса–Лапласа застосовувати не можна, оскільки ці рішення порушують стаціонарність розподілу імовірностей станів природи.