
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклад виконання роботи. Розглянемо приклад виконання роботи за вихідних даних, заданих схемою, наведеною на рисунку 8.5.
|
|
Розглянемо приклад виконання роботи за вихідних даних, заданих схемою, наведеною на рисунку 8.5.
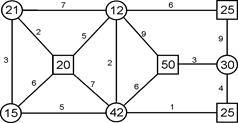
Рисунок 8.5 — Вихідні дані до рішення задачі (приклад)
Розв’язок.
Складаємо довільно початковий план розподілу вантажопотоків (рисунок 8.6). Послідовно призначаємо наступні вантажопотоки:
ланкою (9, 8) направляємо вантажопотік  т;
т;
ланкою (5, 6) направляємо вантажопотік  т;
т;
ланкою (5, 8) направляємо вантажопотік  т;
т;
ланкою (5, 2) направляємо вантажопотік  т;
т;
ланкою (3, 2) направляємо вантажопотік  т;
т;
ланкою (2, 1) направляємо вантажопотік  т;
т;
ланкою (4, 7) направляємо вантажопотік  т;
т;
ланкою (4, 1) направляємо вантажопотік  т.
т.
У складеному початковому плані всі запаси постачальників вивезені та попит одержувачів задоволено. Кількість ланок з вантажопотоком дорівнює 8, що на одиницю менше загальної кількості постачальників та одержувачів. Ланки з вантажопотоком не утворюють замкнений контур. Таким чином, побудований початковий план є допустимим і базисним.

Рисунок 8.6 — Початковий допустимий план перевезень
Розрахуємо транспортну роботу по цьому плану перевезень, склавши добутки вантажопотоків завантажених ланок на їх довжину:
 ткм.
ткм.
Для перевірки цього плану на оптимальність розрахуємо потенціали вершин транспортної мережі (вони записуються біля вершин у дужках поряд з номером вершини). Припишемо вершині 1 початковий потенціал  (можна взяти будь-яке значення, але рекомендується брати початковий потенціал досить великим, щоб надалі не мати справу з від’ємними значеннями потенціалів інших вершин). Послідовно знаходимо потенціали всіх інших вершин:
(можна взяти будь-яке значення, але рекомендується брати початковий потенціал досить великим, щоб надалі не мати справу з від’ємними значеннями потенціалів інших вершин). Послідовно знаходимо потенціали всіх інших вершин:
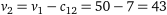 ;
;
 ;
;
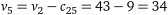 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Для всіх вільних ланок знаходимо значення оцінок  :
:
ланка (1, 7):  ;
;
ланка (2, 4):  ;
;
ланка (4, 8):  ;
;
ланка (2, 8):  ;
;
ланка (7, 8):  ;
;
ланка (3, 6):  ;
;
ланка (6, 9):  .
.
Наявність від’ємних значень оцінок свідчать про те, що складений початковий план не є оптимальним і його можна покращити. Для покращення плану обираємо перспективною ланку (7, 8) з найбільшим за абсолютною величиною від’ємним значенням  . Побудуємо замкнений контур, що утворюють завантажені ланки та перспективна ланка. Контур утворюють ланки 8–7–4–1–2–5–8 (на рисунку 8.6 позначений пунктирними лініями).
. Побудуємо замкнений контур, що утворюють завантажені ланки та перспективна ланка. Контур утворюють ланки 8–7–4–1–2–5–8 (на рисунку 8.6 позначений пунктирними лініями).
Направляємо перспективний вантажопотік від вершини 8 до вершини 7 (оскільки  ), позначаючи його пунктирною стрілкою. Після цього у замкненому контурі переглядаємо завантажені ланки, напрямок вантажопотоку на яких протилежний перспективному. Це ланки: (7, 4) з вантажопотоком
), позначаючи його пунктирною стрілкою. Після цього у замкненому контурі переглядаємо завантажені ланки, напрямок вантажопотоку на яких протилежний перспективному. Це ланки: (7, 4) з вантажопотоком  ; (1, 2) з вантажопотоком
; (1, 2) з вантажопотоком  ; (2, 5) з вантажопотоком
; (2, 5) з вантажопотоком  . Серед цих значень найменшим є вантажопотік
. Серед цих значень найменшим є вантажопотік  , значення якого і приймаємо в якості перспективного (в поліпшеному плані
, значення якого і приймаємо в якості перспективного (в поліпшеному плані  ). У розглядуваному замкненому контурі вантажопотоки
). У розглядуваному замкненому контурі вантажопотоки 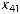 та
та 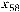 збільшуємо на 3, оскільки вони направлені так же як і перспективний. Вантажопотоки
збільшуємо на 3, оскільки вони направлені так же як і перспективний. Вантажопотоки  ,
,  ,
,  зменшуємо на 3, оскільки вони направлені протилежно перспективному. Після виконаного перерозподілу вантажопотоків ланка (7, 8) стає завантаженою, а ланка (5, 2) стає вільною (рисунок 8.7).
зменшуємо на 3, оскільки вони направлені протилежно перспективному. Після виконаного перерозподілу вантажопотоків ланка (7, 8) стає завантаженою, а ланка (5, 2) стає вільною (рисунок 8.7).

Рисунок 8.7 — План перевезень після першої ітерації
Транспортна робота за цим планом перевезень дорівнює  = 579 ткм, що на
= 579 ткм, що на  ткм менше ніж у попереднього плану. Це зменшення можна розрахувати, помноживши оцінку перспективної ланки на перспективний вантажопотік, тобто
ткм менше ніж у попереднього плану. Це зменшення можна розрахувати, помноживши оцінку перспективної ланки на перспективний вантажопотік, тобто
 .
.
Для отриманого плану знов розраховуємо потенціали вершин та оцінки вільних ланок мережі (рисунок 8.7). План не є оптимальним, оскільки від’ємні значення оцінок мають ланки (1, 7) 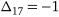 та (2, 8)
та (2, 8)  . Обираємо перспективною ланку (2, 8). Перспективний вантажопотік направляємо від вершини 2 до вершини 8. Замкнений контур утворюють ланки 2–8–7–4–1–2. Найменше значення з вантажопотоків, спрямованих протилежно перспективному, має ланка (4, 7) з
. Обираємо перспективною ланку (2, 8). Перспективний вантажопотік направляємо від вершини 2 до вершини 8. Замкнений контур утворюють ланки 2–8–7–4–1–2. Найменше значення з вантажопотоків, спрямованих протилежно перспективному, має ланка (4, 7) з  . Призначаємо перспективний вантажопотік
. Призначаємо перспективний вантажопотік 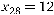 , вантажопотоки
, вантажопотоки  та
та 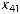 збільшуємо на 12, а вантажопотоки
збільшуємо на 12, а вантажопотоки  та
та  зменшуємо на 12. Переходимо до поліпшеного плану перевезень (рисунок 8.8).
зменшуємо на 12. Переходимо до поліпшеного плану перевезень (рисунок 8.8).

Рисунок 8.8 — Оптимальний план перевезень
Перевірка отриманого плану перевезень показує, що він є оптимальним, оскільки всі оцінки вільних ланок мережі невід’ємні. Транспортна робота оптимального плану W = 531 ткм. Зазначимо, що нульове значення оцінки вільної ланки  вказує на те, що задача має, крім знайденого, ще безліч оптимальних планів, які можна знайти, направивши ланкою (2, 4) вантажопотік (не обов’язково цілочисловий), та перерозподіливши вантажопотоки по замкненому контуру з ланок 2–4–1–2.
вказує на те, що задача має, крім знайденого, ще безліч оптимальних планів, які можна знайти, направивши ланкою (2, 4) вантажопотік (не обов’язково цілочисловий), та перерозподіливши вантажопотоки по замкненому контуру з ланок 2–4–1–2.
Контрольні запитання
1. Дайте постановку транспортної задачі лінійного програмування у сітьовій постановці.
2. Яким вимогам повинен задовольняти початковий допустимий базисний план перевезень?
3. Як розраховуються потенціали вершин мережі?
4. Сформулюйте умову оптимальності плану транспортної задачі у сітковій постановці.
5 Як виконується покращення неоптимального плану транспортної задачі у сітковій постановці?
САМОСТІЙНА РОБОТА №9
ЗАДАЧА ЛИСТОНОШІ
Мета роботи: вивчення алгоритму Фльорі пошуку ейлеревих циклів на графі та алгоритму пошуку найменшого паросполучення алгоритму для розв’язування задачі листоноші.
Стисла теоретична довідка
Задача листоноші у теорії графів пов’язана з пошуком найкоротшого циклу у графі, який проходить кожним ребром графа щонайменше однин раз.
Будемо розглядати зважений орієнтований граф. Зрозуміло, що якщо всі його вершини мають парну степінь, то задача є тривіальною і зводиться до пошуку ейлерева циклу. Знайти його можна, наприклад, за допомогою алгоритму Фльорі.
Алгоритм Фльорі.
1. Розпочати побудови циклу з довільної вершини.
2. Кожне пройдене ребро та утворені при цьому ізольовані вершини закреслюються.
3. У випадку можливості продовження руху декількома ребрами не вибирати ребро, закреслення якого призводить до розбиття графу з не закреслених вершин на декілька незв’язних компонент.
Якщо ж у графі наявні вершини з непарними ступенями (кількість таких вершин завжди є парною), то ейлерів цикл у ньому не існує і деякими ребрами доведеться проходити більш ніж один раз. Нижче наведений алгоритм Крістофідеса для пошуку найкоротшого циклу, що проходить кожним ребром графа з непарними степенями вершин щонайменше один раз.
Крок 1. Нехай  — матриця довжин ребер вихідного графа
— матриця довжин ребер вихідного графа  . Використовуючи алгоритм пошуку найкоротших шляхів (наприклад, алгоритм Дейкстри) побудувати матрицю
. Використовуючи алгоритм пошуку найкоротших шляхів (наприклад, алгоритм Дейкстри) побудувати матрицю  , де
, де  — довжина найкоротшого шляху між вершинами
— довжина найкоротшого шляху між вершинами  та
та  , причому розглядаються тільки вершини, з непарними степенями.
, причому розглядаються тільки вершини, з непарними степенями.
Крок 2. Для матриці найкоротших шляхів  відшукати паросполучення з найменшою сумарною довжиною. За невеликої кількості напарних вершин таке паросполучення можна знайти шляхом перебору варіантів. У супротивному випадку застосовують спеціальні алгоритми.
відшукати паросполучення з найменшою сумарною довжиною. За невеликої кількості напарних вершин таке паросполучення можна знайти шляхом перебору варіантів. У супротивному випадку застосовують спеціальні алгоритми.
Крок 3. Додати додаткові штучні ребра до кожного ребра вздовж найкоротших шляхів, що увійшли до мінімального паросполучення.
Крок 4. У отриманому таким чином графі (всі степені його вершин є парними) відшукати ейлерів цикл за допомого алгоритму Фльорі.
Зміст роботи та вихідні дані до її виконання
Знайти оптимальний (найкоротший) маршрут збирання сміття автомобілем-сміттєвозом на заданій мережі міських вулиць (рисунок 9.1). Довжина вулиць по варіантах наведена у таблиці 9.1.

Рисунок 9.1 — Схема мережі вулиць
Таблиця 9.1 — Вихідні дані до виконання самостійної роботи 9
| Вар. | Довжина вулиць, км | |||||
| a | b | c | d | e | f | |
Продовження таблиці 9.1.
| Вар. | Довжина вулиць, км | |||||
| a | b | c | d | e | f | |