Паралельний метод.

Рішення проводимо за наявної кількості ресурсів у 9 одиниць. Передбачаємо, що на початок кожного дня всі ресурси є вільними.

Перший етап. У перший день маємо можливість виконувати роботи 1–2, 1–3, 1–4. Згідно правил переваги розпочинаємо виконання роботи 1–4 (вона має найменший повний резерв часу та потребує 5 одиниць ресурсу). Роботи 1–2 та 1–3 мають однаковий повний резерв часу, тому згідно третього правила переваги приймаємо рішення розпочати виконання роботи 1–3 (вона потребує більше ресурсо-днів на виконання ніж робота 1–2).

Аналогічним чином діємо для кожного дня до шостого.

Другий етап. На шостий день закінчено виконання роботи 1–3. Є можливість виконувати роботи 1–2, 1–4, 3–5. Згідно правил переваги виконуємо роботу 1–4 (5 одиниць ресурсу) та роботу 1–2 (2 одиниці ресурсу).

Аналогічним чином діємо для кожного дня до восьмого.

Третій етап. На восьмий день закінчено виконання роботи 1–4. Є можливість виконувати роботи 1–2 та 3–5. Загальна потреба у ресурсах для цих робіт не перевищує наявної, тому приймаємо рішення по одночасне виконання цих робіт.

Аналогічним чином діємо для кожного дня до десятого.

Четвертий етап. На десятий день закінчено виконання робіт 1–2 та 3–5. Є можливість виконувати єдину роботу 2–4.

Аналогічно діємо на одинадцятий день.

П’ятий етап. На дванадцятий день закінчено роботу 2–4. Відбулася подія 4. Є можливість виконувати роботи 4–5 та 4–6. Сумарна потреба у ресурсах для цих робіт дозволяє виконувати їх одночасно.

Аналогічним чином діємо для кожного дня до сімнадцятого.

Шостий етап. На сімнадцятий день закінчено виконання роботи 4–6. Однак, подія 6 (завершальна) ще не відбулася. Не відбулася досі подія 5 (роботу 4–5 не закінчено). Розпочати виконання роботу 5–6 немає можливості. Тому продовжуємо виконання роботи 4–5 на вісімнадцятий та дев’ятнадцятий дні.

Сьомий етап. Закінчено виконання роботи 4–5. Відбулася подія 5. Є можливість розпочати останню роботу 5–6 з потребою в ресурсах у 2 одиниці.

Графік виконання робіт і використання ресурсів наведений у таблиці 10.4.

Таблиця 10.4 — Розподіл ресурсів паралельним методом

Таким чином бачимо, що збільшення наявної кількості ресурсів з 8 до 9 дозволяє прискорити виконання комплексу робіт з 28 днів до 22, але все ж не забезпечує технологічний термін його виконання у 18 днів.

Контрольні запитання

1. Поясніть, чому обмеження у ресурсах може зробити неможливим виконання комплексу робіт запланованих згідно їх технологічної послідовності?

2. У чому полягає різниця між послідовним та паралельним методом розподілу ресурсів на мережевих графіках?

3. Сформулюйте суть послідовного методу розподілу ресурсів та правила переваги при виборі робіт для виділення ресурсів за цим методом.

4. Сформулюйте суть паралельного методу розподілу ресурсів та правила переваги при виборі робіт для виділення ресурсів за цим методом.

САМОСТІЙНА РОБОТА №11

РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ ЗА ДОПОМОГОЮ МЕТОДІВ ТЕОРІЇ ІГОР

Мета роботи: вивчення зв’язку між лінійним програмуванням та теорією ігор; вивчення методу розв’язування задач лінійного програмування за допомогою ітеративних наближених методів розв’язування матричних ігор.

Стисла теоретична довідка

Будь-яку матричну парну гру можна розв’язати методами лінійного програмування. Справедливе і зворотне твердження — кожній парі двоїстих задач лінійного програмування можна поставити у відповідність матричну гру, ціна та оптимальні стратегії якої дозволяють обчислити оптимальні плани двоїстих задач (якщо вони існують). При цьому слід зауважити, що у той час, як матричні ігри завжди мають оптимальні стратегії, задачі лінійного програмування можуть і не мати рішень.

Розглянемо пару двоїстих задач лінійного програмування

(1) (2)

; ; .

; ; .

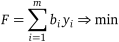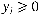Позначимо як

; ; .

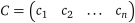Побудуємо гру з платіжною матрицею

,

де є знак транспонування матриці.

Справедлива наступна теорема: пара двоїстих задач лінійного програмування (1)–(2) має розв’язок тоді і тільки тоді, коли гра з платіжною матрицею має таку оптимальну змішану стратегію , що , при цьому

, ; , .

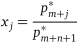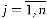Таким чином, рішення пари двоїстих задач лінійного програмування зводиться до визначення оптимальних стратегій гри з симетричною платіжною матрицею порядку .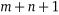

У випадку, коли всі елементи матриці є невід’ємними, а всі компоненти векторів 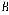і є додатними, можна побудувати еквівалентну матричну гру з платіжною матрицею . Зауважимо, що задача лінійного програмування, для якої виконані ці умови, завжди має розв’язок. Елементи платіжної матриці еквівалентної гри обчислюються за формулою

.

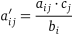Якщо 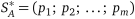— оптимальна стратегія гравця у цій грі, 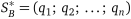— оптимальна стратегія гравця 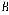у цій грі, а — ціна гри, то оптимальні компоненти розв’язку вихідної задачі лінійного програмування обчислюються за формулами

, ; , .

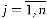Зміст роботи та вихідні дані до її виконання

Розв’язати задачу практичного заняття 2 (вихідні дані до виконання роботи по варіантах наведені у таблиці 2.3 частини ІІ розділу 1), звівши розв’язання задачі лінійного програмування до розв’язання еквівалентної матричної парної гри. Наближений розв’язок гри знайти за допомогою ітеративного методу Брауна-Робінсон (виконати 15 ітерацій за методом).