Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклад виконання роботи. Розв’язати наступну задачу лінійного програмування за допомогою методів теорії ігор:
|
|
Розв’язати наступну задачу лінійного програмування за допомогою методів теорії ігор:
максимізувати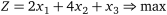 
при обмеженнях
;
;
.
Розв’язок.
Оскільки всі коефіцієнти при невідомих є невідємними, а їх праві частини та коефіцієнти при невідомих у цільовій функції є додатними, складемо платіжну матрицю еквівалентної гри розміром 
:
.
Розв’язуючи цю гру з платіжною матрицею 
методом Брауна-Робінсон отримаємо наближені оптимальні стратегії гравців:
; 
; 
.
Таким чином, наближене оптимальне рішення вихідної задачі лінійного програмування має вигляд
; 
; 
.
Контрольні запитання
1. Наведіть зміст теореми, що відбиває зв’язок між теорями лінійного програмування та ігор?
2. Як побудувати платіжну матрицю еквівалентної гри для довільної задачі лінійного програмування?
3. Яким чином з розв’язку гри отримати оптимальні значення змінних задачі лінійного програмування?
4. За яких умов задача лінійного програмування може бути зведена до еквівалентної гри зменшеного розміру? Яким чином розраховуються елементи платіжної матриці цієї гри? Як знайти оптимальні значення змінних задачі лінійного програмування у цьому випадку?
САМОСТІЙНА РОБОТА №12
ПРИЙНЯТТЯ РІШЕНЬ В УМОВАХ РИЗИКУ
Мета роботи: вивчення методів прийняття рішень в умовах ризику за критерієм очікуваного значення.
Стисла теоретична довідка
Використання критерію очікуваного значення при прийнятті рішень в умовах ризику зумовлено прагненням максимізувати очікуваний прибуток (мінімізувати очікувані витрати). Використання очікуваних величин припускає можливість багаторазового рішення однієї і тієї ж задачі, поки не будуть отримані досить точні розрахункові формули. Математично це виглядає наступним чином.
Нехай 
— випадкова величина з математичним очікуванням 
і дисперсією 
. Якщо 
, 
,..., 
— значення випадкової величини , то середнє арифметичне (вибіркове середнє) значень 
має дисперсію 
. Таким чином, коли 
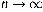то 
і 
.
Інакше кажучи, при досить великому обсязі вибірки різниця між середнім арифметичним і математичним очікуванням наближається до нуля (так звана, гранична теорема теорії імовірності). Отже, використання критерію очікуваного значення справедливе тільки у випадку, коли одне і теж рішення доводиться застосовувати досить велику кількість разів. Вірне і зворотне: орієнтація на очікування буде призводити до невірних результатів для рішень, що доводиться приймати невелику кількість разів.
Зміст роботи та вихідні дані до її виконання
Парк навантажувально-розвантажувальних машин (НРМ) підприємства складається з 
однотипних механізмів. Імовірність виходу з ладу кожної НРМ за 
місяців роботи дорівнює 
. Якщо НРМ виходить з ладу, її ремонтують індивідуально, при цьому середні витрати на ремонт складають 
грн. Керівництво підприємства приймає рішення про проведення планово-попереджувального профілактичного ремонту всіх НРМ через кожні 
місяців на протязі року, при цьому середні витрати на профілактичний ремонт однієї НРМ складають 
грн.
Необхідно визначити, через скільки місяців проводити профілактичний ремонт всіх НРМ, щоб мінімізувати загальні витрати на утримання парку НРМ у робочому стані.
Побудувати також графік очікуваних середніх витрат на утримання парку НРМ в залежності від періоду виконання профілактичних ремонтів .
Вихідні дані до виконання роботи по варіантах наведені у таблиці 12.1.
Таблиця 12.1 — Вихідні дані до виконання самостійної роботи 12
| Вар. | , од.
| Імовірність виходу НРМ з ладу в залежності від
| , грн.
| , грн.
| |||||||||||
| 0, 02 | 0, 09 | 0, 15 | 0, 25 | 0, 30 | 0, 32 | 0, 36 | 0, 45 | 0, 50 | 0, 54 | 0, 58 | 0, 60 | ||||
| 0, 05 | 0, 07 | 0, 09 | 0, 12 | 0, 18 | 0, 24 | 0, 30 | 0, 40 | 0, 42 | 0, 48 | 0, 50 | 0, 52 | ||||
| 0, 03 | 0, 04 | 0, 06 | 0, 11 | 0, 15 | 0, 18 | 0, 20 | 0, 26 | 0, 32 | 0, 38 | 0, 41 | 0, 50 | ||||
| 0, 08 | 0, 10 | 0, 12 | 0, 15 | 0, 25 | 0, 30 | 0, 35 | 0, 40 | 0, 45 | 0, 50 | 0, 55 | 0, 70 | ||||
| 0, 10 | 0, 12 | 0, 16 | 0, 21 | 0, 28 | 0, 30 | 0, 32 | 0, 36 | 0, 40 | 0, 44 | 0, 48 | 0, 56 | ||||