Приклади розв’язання задач. Задача 1. Скласти рівняння дотичних до кола , проведених з точки .

Задача 1. Скласти рівняння дотичних до кола , проведених з точки .

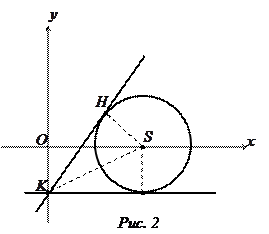
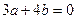Розв’язання. І спосіб. Перетворимо рівняння кола до виду , що дозволяє знайти центр кола - точку та його радіус . Складемо рівняння пучка прямих з центром в точці K: та підберемо параметри та так, щоб прямі із одержаного пучка проходили на відстані 1 від точки . Користуючись формулою відстані від точки до прямої, дістаємо , або , звідки після спрощень дістаємо або . При 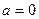із рівняння пучка дістаємо перший розв’язок: . Одним з ненульових розв’язків рівняння 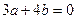є . Це дозволяє отримати другий розв’язок задачі: .

Відповідь. .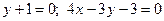

ІІ спосіб. Оскільки та , то з прямокутного трикутника (рис. 2) відрізок KH дотичної, проведеної з точки до кола, рівний 2, тому дотичні до кола утворюють з прямою KS кут , для якого . Рівняння прямої KS запишемо у виді рівняння прямої у відрізках на осях 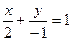, або . Кутовий коефіцієнт одержаної прямої буде . Запишемо рівняння пучка з центром у точці K у виді (при цьому з розгляду випадає пряма 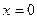, але, як легко бачити, вона не є дотичною до кола). Виберемо з одержаного пучка дві прямі, виходячи з умови, що вони утворюють з прямою KS кут , де 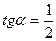. Скориставшись формулою для відшукання кута між двома прямими у виді , дістаємо , звідки . Розв’язуючи одержане рівняння, знаходимо . Підставивши значення в рівняння пучка, отримуємо попередню відповідь.

ІІІ спосіб. Скористаємось записаним вище рівнянням пучка прямих і виберемо параметр так, щоб система

мала єдиний розв’язок (дотична з колом мають єдину спільну точку). Розв’язуючи систему, дістаємо рівняння . Оскільки його дискримінант 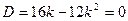, то 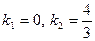. Залишається підставити одержані значення у рівняння пучка та одержати попередню відповідь.

ІV спосіб. Складемо рівняння кола з діаметром KS. Центр його буде знаходитися в точці , а радіус . Отримаєм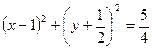о , або . Точки перетину одержаного кола, та кола, заданого в умові задачі, належать шуканим дотичним. Розв’язуючи систему

,

дістаємо

Склавши рівняння прямих, які проходять через кожну з одержаних точок та точку S, дістаємо попередню відповідь.

Задача 2. Скласти рівняння бісектриси того із кутів, утворених при перетині прямих 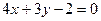та 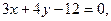якому належить точка .

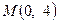Розв’язання. Всі точки кута рівновіддалені від сторін кута. Тому, якщо точка належить бісектрисі, то виконується рівність , звідки . З двох одержаних співвідношень отримуємо рівняння бісектрис двох суміжних кутів: та . Візьмемо на першій із них довільну точку, нехай та встановимо, як розташовані точки та відносно сторін кута. Для координат точки вирази та додатні, для координат точки - теж. Це означає, що точки та лежать в одному куті.

Відповідь. .

Задача 3. Задати аналітично множину точок, розташованих між паралельними прямими 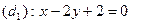та .

Розв’язання. Візьмемо на прямій точку та встановимо знак виразу . Оскільки в точці вираз від’ємний, то нерівність задає півплощину, яка містить пряму та обмежена прямою Аналогічно, вибравши точку на прямій , встановлюємо, що вираз в даній точці приймає додатне значення, тобто нерівність задає півплощину, яка містить пряму . Точки, розташовані між прямими, є спільними точками одержаних півплощин.

Відповідь.