Метод Порето

Для сужения области поиска оптимальных решений применяется также алгоритм выделения множества точек (области) Порето. Опреде­ление системы весовых коэффициентов W_i и районирование по ней решений из области Порето позволяет получить оптимальный компромиссный вариант, сбалансированный по противоречивости относительно совокупности критериев F_i проектирования, или показателей свойств объекта. Точками Порето являются точки пространства решений , для которых выполняется условие

.

Таким образом, точки области Порето представляют собой перспективные варианты решения. Для существования области Порето, т.е. для , необходимо, чтобы существовало также множество весов

W = (W₁, …, W_m), W_i > 0;

, grad (∑ W_i F_i) = 0,

что позволяет сформировать комплексную целевую функцию

и минимизировать ее в программе для получения точек множества Порето .

Задачу минимизации можно также сформулировать как задачу мини­мизации функционала

в пространстве частных критериев , где Q - область допустимых или реализуемых решений. При этом определяется точка так, что ее проекция W является наименьшей среди всех . В этом случае F (x_n) лежит на границе Q и функционал π определяет плоскость касательную в точке Порето x_h и поддерживающую область Q.

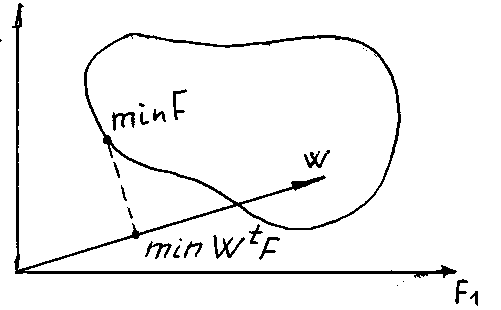
Рис.5.2. Выбор точки множества Порето

Предположим, что минимизацией функционала π при использовании различных векторов весов W¹, …, W^m получены m точек множества Порето . Тогда это множество весов и точек образует выпуклую кусочно-линейную аппроксимацию F_n (x_n) для области F (x_n).

Рис.5.3. Построение аппроксимирующей поверхности

Таким образом, область Порето может быть представлена выпуклой лицевой оболочкой F_H, образуемой ограничивающими ее гипер­плоскостями, заданными внешними нормалями. Нормаль к такой поверхности получают формированием матрицы

F = и решением уравнения

F ^tW^* = e, где e = (1, 1, …, 1)^t.

Таким образом, лицевая сторона оболочки F_H задается точками такими, что F ^tW^* = 1. Отсюда можно найти новые точки Порето …

Начальное опорное множество точек Порето , получают
минимизацией каждого из частных критериев F_i в предположении, что
множество весов Wⁱ соответствует вектору, все компоненты которого
равны нулю за исключением W_i = 1.

Следующий шаг предполагает определение весов W ^{( m+k )}, которые в соответствии с принципом Порето обеспечивают компромисс между частными критериями F_i. Поскольку компромиссная поверхность Порете проходит через m экстремальных точек, соответствующих F_imin и образующих лицевую сторону аппроксимации F_H, согласно (I) запишем:

.

Найденный вектор весов W, представляющий собой нормаль к поверхности Порето, используется при последующей минимизации всего аддитивного критерия для получения дополнительной (m +1)-й точки Порето F_m+1. Если это решение неудовлетворительно, на­пример из-за большого j -го слагаемого, то производится замена на F_m+1 и процедура нахождения нормали W ^* по уравнению (I) повторяется.

Значения весовых коэффициентов частных критериев W_К определяются, как правило, экспертизой на основании использования коллективного опыта.