Статистическая оценка тормозной динамичности автомобиля

Торможение автомобиля представляет собой сложный процесс. Он протекает под воздействием большого числа факторов, различных по характеру, интенсивности и про­должительности действия. Многие факторы связаны между собой сложными функциональными зависимостя­ми, не всегда поддающимися учету. При эксперимен­тальном определении отдельных параметров всегда полу­чают не одно конкретное значение, а некоторое их мно­жество, характеризуемое определенным законом распре­деления. При торможении автомобиля каждый из эле­ментов этого множества может случайным образом всту­пить в сочетание с любым элементом другого множества, поэтому и значения характеристик торможения (например, замедления и тормозного пути) являются случайными. Так, многократное торможение автомобиля на том же участке дороги никогда не дает в точности совпадаю­щих результатов, несмотря на постоянство условий испы­таний. Расхождения между значениями тормозного пути при отдельных замерах могут достигать 15—20%.

Для полной оценки случайных значений необходимо располагать большим количеством реализаций случайного процесса. Однако при анализе ДТП эксперт имеет сведения лишь об одной реализации (длине следов юза) и должен по ней определить начальную скорость авто­мобиля. Если считать это значение абсолютно достовер­ным, а применяемые формулы точными, то и единствен­ное значение скорости, полученное расчетом, следует признать достоверным, хотя оно является лишь одним из множества возможных значений. Для полной оценки результата необходимо знать не только дискретное значение параметра, но и закон распределения случайных показателей, а также границы интервала, в которых это значение может находиться. Тогда, используя мето­ды теории случайных процессов, можно определить точность проведенного расчета и степень надежности полученного решения. Статистические методы исследова­ния широко применяются в промышленности, связи и других отраслях народного хозяйства.

Подробный анализ торможения автомобиля как случайного про­цесса проведен исследователями И. К. Пчелиным и Е. И. Кали­ниным. В качестве примера рассмотрим использование вероятност­ных методов для определения тормозного пути и начальной скорости автомобиля. Для простоты, пренебрегая кратким переходным процес­сом (увеличением замедления за время t ₃), ограничимся рассмотре­нием лишь одного случайного показателя — коэффициента сцепления. Согласно многочисленным исследованиям коэффициент сцепления слу­чайным образом меняется по направлению движения автомобиля Значения 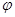_х, замеренные через 15—20 см тормозного пути, могут иметь разброс 30—50%, и коэффициент продольного сцепления можно считать случайной функцией перемещения автомобиля, подчиняющейся нормальному (Гауссовскому) закону распределения

Случайная функция оценивается по среднему значению (мате­матическому ожиданию 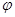_т), среднему квадратическому отклонению , корреляционной функции или спектральной плотности.

Пусть эти характеристики известны нам из опыта. Тогда приме­нение теории случайных процессов к исследуемому вопросу дает следующую формулу для определения границ интервала, в котором может находиться начальная скорость автомобиля, если известно значение тормозного пути S _ю:

(3.42)

Среднее квадратическое отклонение

(3.43)

где D , — дисперсия случайной функции сцепления; и — коэффи­циенты корреляционной связи, определяемые из опыта. Формула (3.43) получена в предположении, что корреляционная

функция коэффициента сцепления аппроксимирована выражением:

Таким образом, если известны длина тормозного следа S _ю, остав­ленного на покрытии, и статистические характеристики коэффициен­та сцепления для данного участка дороги, то по выражению (3.42) можно оценить, как велики могут быть отклонения скорости от среднего значения. Интервал ±3 . соответствующий при нормальном законе распределения вероятности 0, 997, часто используют в практике.

Определим, например, какое значение могла иметь скорость авто­мобиля, если длина следа юза S _ю =34, 0 м. Среднее значение коэффи­циента сцепления =0, 6, а покрытие дороги характеризуется парамет­рами: D ₁ =0, 006; =0, 4 1/м; =0, 3 1/м.

Среднее квадратическое отклонение по формуле (3.43) Значение начальной скорости находится в пределах [см. формулу (3.42)]: 18, 8 м/с 21, 2 м/с. При вычислении по среднему значению коэффициента сцепления

(0, 6) =20 м/с.

Таким образом, фактическая скорость автомобиля может отличать­ся от скорости, вычисленной по применяемым в настоящее время формулам, на ±6%. При других характеристиках покрытия разброс значений может быть намного больше.

Соотношение (3.42) можно также использовать для решения обрат­ной задачи: по известной скорости найти границы интервала, в кото­рых находятся возможные значения тормозного пути. Для этого нужно решить формулу (3.42) относительно S _ю. Проще всего это можно сделать, применяя метод последовательных приближений. В качестве первого приближения можно принять

(3.44)

Процесс быстро сходится и обычно достаточно одного шага. Тогда искомое значение тормозного пути находится в пределах

(3.45)

Так, например, если начальная скорость автомобиля равна 20 м/с, а участок дороги имеет характеристики сцепления, приведенные выше, то согласно формуле (3.44) S _ю1 =400/(2*9, 81* 0, 6) =34, 0 м. При вычис­ленном ранее значении среднего квадратического отклонения =0, 024 границы интервала, в которых может находиться истинное значение тормозного пути, будут: 30, 4 м 38, 6 м. Таким образом, откло­нения от значения S _ю, вычисленного по среднему значению , равны ±12%.

Внедрению статистических методов исследования ДТП препятствует, с одной стороны, их сложность, с другой — отсутствие экспериментальных данных о характеристиках случайных функций, влияющих на процесс торможения (D ; а ; и др.).

Длина остановочного пути автомобиля зависит не только от коэффициента сцепления, но и от многих других параметров. Так, входящие в формулу (3.16) зна­чения времени t ₁, t ₂, t ₃ также являются случайными функциями многих аргументов. С учетом общих тенденций развития науки внедрение статистических методов в буду­щем представляется неизбежным, хотя предстоит еще большая работа по накоплению экспериментального ма­териала и выявлению основных закономерностей.

Контрольные вопросы

1. Что понимают под расчетом движения автомобиля?

2. Как определить параметры движения автомобиля накатом?

3. Каким образом рассчитать путь, время и скорость движения автомобиля при торможении двигателем?

4. От каких факторов зависит коэффициент сцепления шин с дорогой? Назовите примерные его значения для разных покрытий.

5. Нарисуйте и объясните тормозную диаграмму.

6. Какая разница между тормозным и остановочным путями автомобиля?

7. От каких факторов зависит время реакции водителя, в каких пределах оно изменяется?

8. Что называют временем запаздывания тормозного привода и временем нарастания замедления?

9. Как определить замедление автомобиля при торможении его на двух участках с разными коэффициентами сцепления?

10. В чем особенность расчета движения автомобиля при торможе­нии его без блокировки колес?

11. Опишите методику статистической оценки параметров торможе­ния.