Введение метрики в евклидовом пространстве

Пусть Е_n – n- мерное евклидово пространство. Скалярное произведение вектора самого на себя назовём скалярным квадратом этого вектора, т.е. (а, а) = а². По 4-ой аксиоме скалярного произведения а² ³ 0.

Определение 47. Длиной вектора называется арифметическое значение квадратного корня из скалярного квадрата этого вектора. т.е. ú а ú = (44)

Свойства длины вектора:

1. Любой вектор а имеет длину и только одну, ú а ú ³ 0.

2. ú a× а ú = ú aú × ú а ú для любого а Î Е_n.

3. Для любых векторов а и в из Е_n верно неравенство ú а× в ú £ ú а ú × ú в ú.

Доказательство. (а – a в)² = а ² – 2a(а, в) + a²× в ² ³ 0 для любого a Î R. Так как квадратный трёхчлен неотрицателен при любом значении a, то его дискриминант неположителен, т.е. (а, в)² – а ²× в ² £ 0, или (а, в)² £ а ²× в ². Отсюда ú а× в ú £ ú а ú × ú в ú (45). Знак равенства в этой формуле будет тогда и только тогда, когда векторы пропорциональны.

Определение 48. Вектор единичной длины называется единичным вектором или ортом.

4⁰. Для любого ненулевого вектора существует пропорциональный с ним орт.

Если а ¹ 0, то ú а ú ¹ 0. Следовательно, существует вектор а₀ = 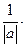а. Очевидно, ú а₀ ú =1.

Определение 49. Углом между ненулевыми векторами а и называется такое действительное число j, что (46).

Угол между векторами а и можно также обозначать .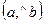

Свойства углов.

1⁰. Для любых двух ненулевых векторов угол между ними определён.

Из формулы (45) следует, что Следовательно, j существует.

2⁰. Если a ¹ 0, b ¹ 0, то .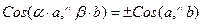

Определение 48. Два ненулевых вектора называются ортогональными, если их скалярное произведение равно нулю.

4⁰. Если а ^ в и а ^ с и в + с ¹ 0, то а ^ (в + с).

Определение 50. Множество всех векторов пространства Е_n, ортогональных вектору а, к которому добавлен нулевой вектор, называется ортогональным дополнением вектора а.

5⁰. Ортогональное дополнение к вектору а является (n – 1)-мерным евклидовым подпространством в Е_n.

Доказательство.

Из свойств 3⁰ и 4⁰ следует, что рассматриваемое множество L является линейным подпространством в Е_n. Так как в Е_n определено скалярное произведение, то оно определено и в ортогональном дополнении, следовательно, L является евклидовым подпространством. Кроме того, с Î L Û (а, с) = 0 (*). Зафиксируем в Е_n базис. Пусть а = (а₁, а₂, …, а_n), с = (х₁, х₂, …, х_n). Тогда с Î L Û а ^Т× Г× х = 0 (**). Уравнение (**) есть линейное однородное уравнение с n неизвестными. Фундаментальная система его решений состоит из (n – 1) решения. Следовательно, пространство решений уравнения (**) является (n – 1)-мерным.

Пусть Е_к – подпространство пространства Е_n. Обозначим Е множество, состоящее из нулевого вектора и всех векторов, ортогональных любому ненулевому вектору из Е_к. Иными словами с Î Е Û (с, а) = 0 для всех а Î Е_к. Пространство Е ортогональным дополнением к пространству Е_к.

6⁰. Ортогональное дополнение Е является (n – к)-мерным евклидовым подпространством в пространстве Е_n.

Доказательство аналогично доказательству свойства 5⁰.

7⁰. Е Ç Е_к = { 0 }.

8⁰. Любые два ортогональных вектора линейно независимы.

Доказательство. Пусть а ^ в. По определению эти векторы ненулевые. Предположим, что они линейно зависимы, т.е. существует такая ненулевая пара a, b действительных чисел, что a× а + b× в = 0. Если a ¹ 0, то умножим обе части последнего равенства скалярно на вектор а. Получим a× а² + b× (а, в) = 0. Так как (а, в) = 0 и а² ¹ 0, то a = 0. Противоречие. Следовательно, а и в линейно независимы.

9⁰. Если а₁, а₂, …, а_к и в₁, в₂, …, в_s – две системы линейно независимых векторов и каждый вектор первой системы ортогонален любому вектору второй, то система векторов а₁, а₂, …, а_к, в₁, в₂, …, в_s линейно независима.

Теорема 42. Для любого к (1 £ к £ n) Е_n = Е Å Е_к.

Доказательство. Пусть (е₁, е₂,..., е_к) – базис в Е_к и (е_{к +1}, е _{к + 2},..., е_n) – базис в Е . Из свойства 9⁰ следует, что (е₁, е₂,..., е_к, е_{к +1}, е _{к + 2},..., е_n) будет линейно независимой. Так как в ней n векторов, то это базис в Е_n. Следовательно, Е_n = Е + Е_к. Из свойства 7⁰ следует Е_n = Е Å Е_к.

Пусть Е_n = Е Å Е_к. Если а – любой вектор из Е_n, то а = а₁ + а₂, где а₁ Î Е_к, а₂ Î Е . Вектор а₁ называется проекцией вектора а на подпространство Е_к. Вектор а₂ называется ортогональной составляющей вектора а.