Объем куба и прямоугольного параллелепипеда.

Рассмотрим куб, принятый за единицу измерения объемов. Его ребро равно единице измерения отрезков. Разобьем каждое ребро этого куба на n равных частей, где n – произвольное целое число, и проведем через точки разбиения плоскости, перпендикулярные к этому ребру. Куб разобьется на n³ равных кубиков с ребром 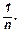Так как сумма объемов всех маленьких кубиков равна объему всего куба, т. е. равна 1, то объем каждого из маленьких кубиков равен Объемы маленьких кубиков равны друг другу, так как соответственно равны длины их ребер.

Объем куба с ребром 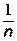равен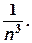

Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений:

где а – длина, b – ширина, h – высота прямоугольного параллелепипеда.

Для доказательства воспользуемся принципом Кавальери.

1) Сначала найдем объем прямоугольного параллелепипеда со сторонами основания a, b и высотой 1. Расположим единичный куб и данный параллелепипед так, чтобы их основания находились в одной плоскости, а сами многогранники были расположены по одну сторону от этой плоскости. Тогда любая плоскость, параллельная плоскости оснований этих многогранников и пересекающая куб, пересекает также и прямоугольный параллелепипед, причем площади сечений, образованных при пересечении обоих многогранников, относятся как 1: (ab). Это означает, что объемы этих тел относятся как 1: (ab). Иными словами, если объем единичного куба равен 1, то объем рассматриваемого прямоугольного параллелепипеда равен V = ab.

2) Теперь найдем объем прямоугольного параллелепипеда с измерениями a, b, h. Расположим прямоугольный параллелепипед с измерениями a, b, 1 и прямоугольный параллелепипед с измерениями a, b, h так, чтобы грань со сторонами 1 и а и грань со сторонами h и a находились в одной плоскости, а сами параллелепипеды были расположены по одну сторону от этой плоскости. Тогда любая плоскость, параллельная плоскости оснований этих параллелепипедов и пересекающая первый из них, пересекает также и второй параллелепипед, причем площади сечений, образованных при пересечении обоих многогранников, относятся как (1× a): (ah) = 1: h. Это означает, что объемы этих тел относятся как 1: h. Таким образом, если объем первого параллелепипеда равен ab, то объем второго прямоугольного параллелепипеда равен V = abh.

Следствия:

1.Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

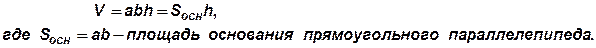
2.Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. Для доказательства этого утверждения достроим прямую треугольную призму до прямоугольного параллелепипеда. Объем этого параллелепипеда равен 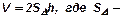площадь треугольника, лежащего в основании. Секущая плоскость разбивает параллелепипед на две равные прямые треугольные призмы, поэтому объем призмы равен половине объема прямоугольного параллелепипеда.