Теоретическая часть

СПЕКТРАЛЬНЫЙ АНАЛИЗ Действительных случайных сигналов.

Цель работы: изучить и численно исследовать спектральные и корреляционные характеристики случайных сигналов;

Теоретическая часть

Сигналом называют процесс изменения во времени физического состояния какого-либо объекта, служащий для отображения, регистрации и передачи сообщений.

Спектральное представление сигнала 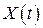представляет собой разложение его на сумму (конечную или бесконечную) элементарных гармонических сигналов с различными частотами. Спектральное представление как непериодических детерминированных, так и стационарных случайных, сигналов осуществляется путём разложения их в интеграл Фурье. В частотной области такие процессы характеризуются своим спектром 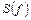. Процесс 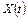и его спектр 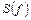взаимно связаны парой преобразований Фурье (соответственно прямым и обратным):

, .

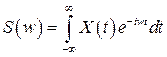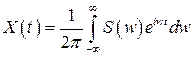Корреляционная функция стационарного случайного процесса 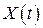есть функция сдвига между аргументами: 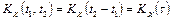. Она обладает следующими свойствами:

1) ;

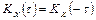2) ;

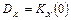3)

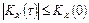
Стационарный случайный процесс 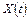называют эргодическим, если его характеристики (математическое ожидание, дисперсия и корреляционная функция), найденные усреднением множества реализаций, совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации 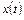, которая наблюдалась на интервале достаточно большой длительности.

В качестве оценки корреляционной функции эргодического процесса 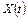, представленного своей временной реализацией 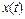длины 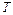принимают

.

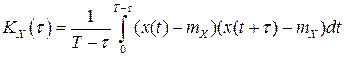Числовой характеристикой, служащей для оценки скорости изменения реализации случайного процесса, является интервал корреляции :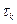

.

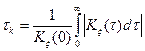Если известна информация о поведении какой-либо реализации в прошлом, то возможен вероятностный прогноз на время .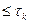

Спектральной плотностью (спектром мощности) стационарного случайного процесса 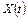называют функцию 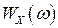, которая связана с корреляционной функцией 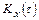взаимно обратными преобразованиями Фурье:

, .

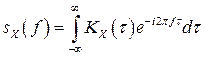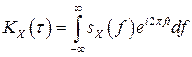Спектральная плотность стационарного случайного процесса 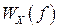обладает следующими свойствами:

1) если процесс 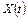- вещественный, то ;

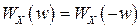2) 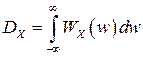. Спектральная плотность описывает распределение дисперсий случайного процесса по непрерывно изменяющейся частоте .

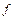3) .

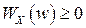Для действительных процессов выполняется:

.

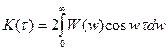
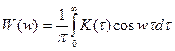Эффективной шириной спектраназывается величина 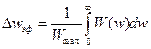. Вне пределов эффективной ширины спектра спектральную плотность мощности считают равной 0.

При численном моделировании (обработке) процессов непрерывный во времени сигнал заменяется дискретным рядом. Когда реализация 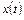представлена временным рядом с интервалом дискретизации 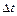, длина реализации 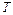связана с объёмом выборки 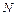равенством 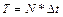. Предполагается, что рассматриваемая реализация имеет периодический характер и период её равен 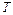. Непрерывная реализация 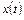заменяется временным рядом 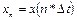, где 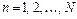, а непрерывное преобразование Фурье 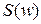– дискретной последовательностью 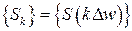, 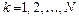. Соответствующая пара преобразований Фурье определяется формулами

, ,

, .

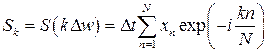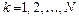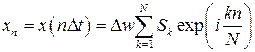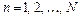Свойства ДПФ

1. ДПФ — линейно, т.е. сумме сигналов соответствует сумма их спектров.

2. 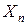и 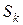— периодические функции по модулю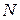

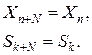
3. 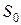— постоянная составляющая

.

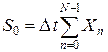4. Для действительных процессов, т.к. 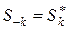спектр симметричен

.

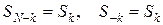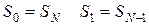
Вычисление спектральной плотности по временной реализации через преобразования Фурье

Пусть имеются 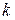реализаций случайного процесса длиной 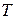, и для каждой вычислен спектр

,

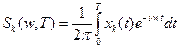тогда

.

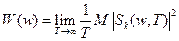Периодограмный метод позволяет получать оценку спектральной плотности непосредственно по исходному набору данных. Для того чтобы получить статистически устойчивую спектральную оценку, имеющиеся массив данных необходимо разбить на перекрывающиеся сегменты и в последующем усреднить выборочные спектры, полученные по каждому такому сегменту. Параметры этого усреднения изменяются посредством соответствующего выбора числа отсчетов на сегмент (NSАМР) и число отсчетов, на которое необходимо сдвинуть начало следующего сегмента (NSHIFT). Обычно NSHIFT= NSАМР/2.

При малом значении параметра NSАМР получается больше сегментов, по которым будет производиться усреднение, а следовательно, будут получаться оценки с меньшей дисперсией, но также и с меньшим разрешением. Увеличение параметра NSАМР повышает спектральное разрешение, но, естественно, за счет увеличения дисперсии из-за меньшего числа усредняемых сегментов.

Процедура, которая начинается с использования низкого разрешения и высокой устойчивости, с последующим переходом к периодограмным оценкам с большим разрешением и более низкой устойчивостью называется закрытием (т. е. уменьшением размера) окна. Это название относится к ширине окна, которая устанавливается посредством выбора параметра NSАМР. Закрытие окна достигается за счет уменьшения числа сегментов при одновременном увеличении их длины.