Проверка гипотез о виде распределения

Статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то есть, чем больше ее наблюдаемое значение 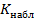, тем сильнее довод против основной гипотезы.

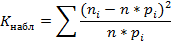
Поэтому критическая область для этой статистики всегда правосторонняя: [ ; +∞).

Её граница 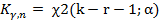находится по таблице распределения «хи-квадрат», используя значения k (число интервалов), r (количество параметров, участвующих в оценивании). Например, для нормального распределения количество параметров 2: , следовательно, r=2.

1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.

Для вычисления вероятностей 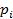применим формулу и таблицу функции Лапласа

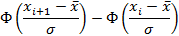
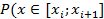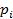
Группы	Количество, ni	,	Ожидаемая частота,	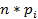Слагаемые статистики Пирсона
8 - 33.33		0, 23522	47, 044	225, 320
33.33 - 58.66		0, 26651	53, 302	53, 302
58.66 - 83.99		0, 19182	38, 364	25, 641
83.99 - 109.32		0, 08697	17, 394	26, 838
109.32 - 134.65		0, 02497	4, 994	1, 795
134.65 - 159.98		0, 00452	0, 904	0, 904
159.98 - 185.31		0, 00052	0, 104	0, 104
185.31 - 210.64		0, 00003	0, 006	0, 006
210.64 - 235.97		0, 00001	0, 002	1996, 002
Сумма				2329, 912

Границу находим по таблице распределения «хи-квадрат», используя значения k=9, r=2.

= 12.59159;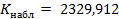

Наблюдаемое значение статистики Пирсона попадает в критическую область: 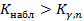, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.

2. Проверим гипотезу о том, что Х распределено по закону Пуассона.

Для вычисления вероятностей 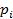применим следующую формулу:

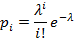
, где; .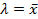

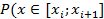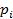
Группы	Количество, ni	,	Ожидаемая частота,	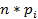Слагаемые статистики Пирсона
8 - 33.33
33.33 - 58.66
58.66 - 83.99
83.99 - 109.32
109.32 - 134.65
134.65 - 159.98
159.98 - 185.31
185.31 - 210.64
210.64 - 235.97
Сумма

Границу находим по таблице распределения «хи-квадрат», используя значения k=9, r=1.

= 23.58935;

Наблюдаемое значение статистики Пирсона не попадает в критическую область: 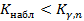, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют распределение Пуассона.

3. Проверим гипотезу о показательном распределении генеральной совокупности.

Для вычисления вероятностей 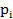применим следующую формулу:

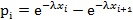
, где; .

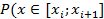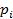
Группы	Количество, ni	,	Ожидаемая частота,	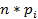Слагаемые статистики Пирсона
8 - 33.33		0, 384096327	76, 81926531	69, 71454
33.33 - 58.66		0, 203902792	40, 78055844	40, 78056
58.66 - 83.99		0, 108244588	21, 64891763	9, 91231
83.99 - 109.32		0, 057463121	11, 49262424	65, 83838
109.32 - 134.65		0, 030505084	6, 101016881	2, 756645
134.65 - 159.98		0, 016194042	3, 238808318	3, 238808
159.98 - 185.31		0, 008596829	1, 719365726	1, 719366
185.31 - 210.64		0, 004563744	0, 912748829	0, 912749
210.64 - 235.97		0, 002424781	0, 48495628	4, 733122
Сумма				199, 6065

Границу находим по таблице распределения «хи-квадрат», используя значения k=9, r=1

= 12.59159;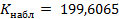

Наблюдаемое значение статистики Пирсона попадает в критическую область: 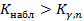, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по показательному закону.