
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет пространственных стержневых систем.
|
|
Класс стержневых систем по взаимному расположению элементов и внешних нагрузок делится на три группы: плоские, плоскопространственные и пространственные. В первой группе все стержни и силы расположены в одной плоскости. Во второй группе стержни системы расположены в одной плоскости, а силы – в другой (как правило перпендикулярной первой). В третьей группе стержни и силы могут располагаться в произвольных плоскостях (как минимум трех взаимно ортогональных).
Р F
Р
Р
F
а) б) в)
Рамы: а – плоская; б – плоскопространственная; в – пространственная.
а) б)
Р
Р
Простейшие фермы: а – плоская, б – пространственная.
Плоские рамы и фермы не используются в строительстве поодиночке, так как они не устойчивы в направлении, перпендикулярном конструктивной плоскости. Такие рамы и фермы выделяются из пространственных конструкций с целью упрощения последних.
Плоско-пространственные рамы (рис. (б)) являются самостоятельными конструкциями (балконные рамы, несущие рамы автомобилей и электровозов и др.). Эти рамы статически неопределимы и для их раскрытия используется метод сил. Если раму (б), для которой n=6, мысленно разрезать в произвольном сечении, то в общем случае нагружения необходимо ввести шесть неизвестных внутренних усилий: x1=N – продольная сила, x2=Qx и x3=Qy – поперечные силы, x4=Mk - крутящий момент, x5=Mx и x6=My – изгибающие моменты. Для частного случая симметричного нагружения конструктивно симметричной рамы, необходимо выбрать симметричную основную систему. В таком случае антисимметричные неизвестные исчезнут: x2=x3=x4=0, кроме того от действия вертикальной нагрузки будут равны нулю продольная сила x1=0 и изгибающий момент в горизонтальной плоскости x6=0. Остается неизвестным изгибающий момент в вертикальной плоскости x5.
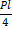
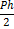
|
Эп.MkF
h Эп.MxF 1 1 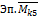
| x6 |
| x5 |
| x5 |
 x3
x3
| x4 |
| x2 |

|
x Эп.MxF 1 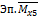 x1
x1
z
Каноническое уравнение метода сил имеет вид:
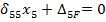
Построив единичные и грузовые эпюры изгибающих и крутящих моментов, можно вычислить податливость 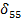 и перемещение
и перемещение 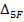 :
:
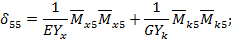
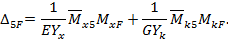
Модуль сдвига можно заменить модулем Юнга:
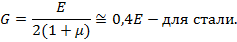
Момент инерции при кручении можно заменить осевым моментом инерции:
· Для круга: 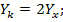
· Для прямоугольника: 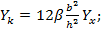
· Для квадрата: 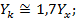
· Для двутавра: 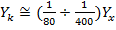 - в зависимости от номера I.
- в зависимости от номера I.
Дальнейшее решение задачи аналогично расчету плоских рам. Пространственная рама (b) в общем случае нагружения 18 раз статически неопределима. Для частного случая нагружения решение упрощается. Например, при антисимметричном нагружении силами F (P=0) число неизвестных при выборе симметричной основной системы снижается до трех, т.е. в 6 раз.
При расчете пространственных ферм предполагается, что все стержни соединены в узлах шаровыми шарнирами. Это обеспечивает работу элементов только на растяжение или сжатие от действия узловых нагрузок. Опоры пространственных ферм делятся на три типа:
1. Шаровая подвижная опора;
2. Шаровая подвижная опора на цилиндрических катках;
3. Шаровая подвижная опора на шаровых катках.
c
| e |
| d |
| a |
| b |
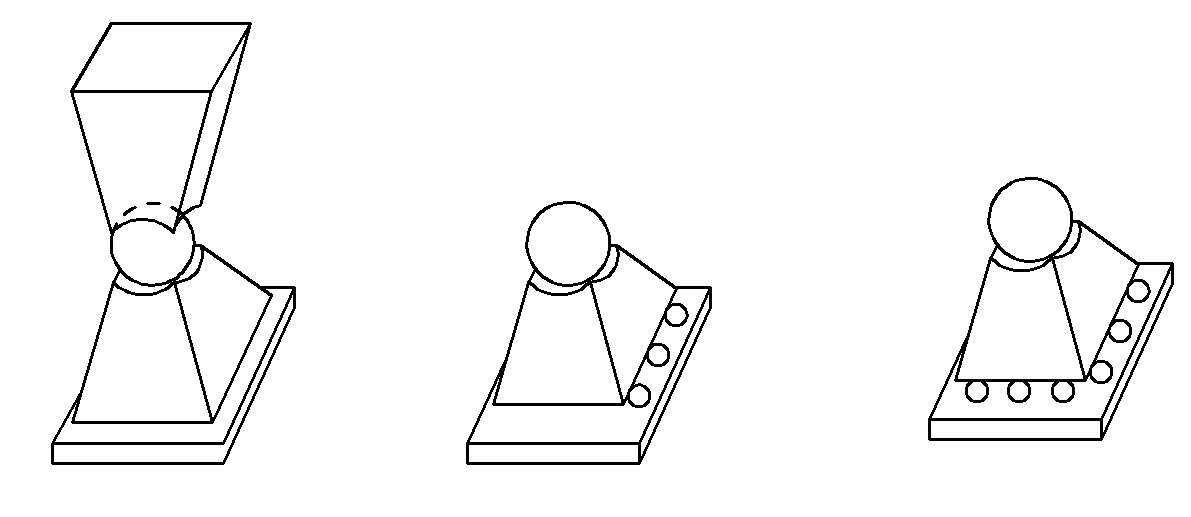
1) 2) 3)
Rz Ry Rz Rz
Rx Rx
a – шаровой шарнир;
b – опорная подушка;
c – узел фермы;
d – цилиндрические катки;
e – шаровые катки.
Выше мы назвали диском любую геометрически неизменяемую плоскую ферму. Аналогично назовем блоком любую геометрически неизменяемую пространственную ферму. Незакрепленный диск имеет 3 степени свободы, а незакрепленный блок 6 степеней свободы.
Для неизменяемого прикрепления блока к земле, т.е. создания инженерного сооружения, необходимо использовать 6 опорных стержней, расположенных не менее чем в трех точках. Покажем классическое закрепление.
| RBX блок |
| т.А – трехстержневая опора (I тип) т. B – двухстержневая опора (II тип) т. С – одностержневая опора (III тип) |
| RAZ |
| R |
| A |
| RCZ |
| RAX |
C
При расстановке опор необходимо учитывать следующие ограничения:
· Три стержня 1, 2, 3 опоры А не должны распологаться в одной плоскости;
· Плоскость стержней 4, 5 опоры В не должна проходить через т. А;
· Направление стержня 6 опоры С не должно пересекать линию АВ.
Опорные реакции определяют из уравнений равновесия:
Заменяя Землю блоком, получаем аналогичное правило неизменяемого соединения двух блоков.
Простейшие пространственные фермы имеют регулярную структуру в виде последовательного прикрепления каждого узла тремя стержнями, не лежащими в одной плоскости (рис.а).
Простейший блок имеет вид тетраэдра, имеющего 6 стержней (рис.б). более сложный блок можно получить последовательным присоединением новых узлов (рис.в).
G
D D H I
A B A B E F
C C
A B
a) б) в) C D
Получим структурную формулу для геометрической неизменяемости фермы. Обозначим S – число стержней, U – число узлов. Для основного блока имеем S0=6; U0=4. Для последующих (U-4) узлов необходимо поставить 3(U-4) стержня. Общее количество стержней пространственной фермы: S=6+3(U-4)=3U-6 (1).
Для сооружения, т.е. фермы, прикрепленной к земле 6 стержнями, получаем:
S=3U-6+6=3U, т.е. S=3U (1.а)
Формулы (1) и (1.а) являются необходимыми и достаточными условиями существования блока и сооружения при рассмотренном способе образования фермы и прикреплении ее к земле.
Если используются другие способы образования блока и его крепления к земле, то эти формулы определяют только необходимое, но не достаточное условие геометрической неизменяемости.
Для окончательного заключения о неизменяемости необходимо провести анализ структуры системы или дать аналитическое исследование определенности усилий при действии произвольной нагрузки. Одним из способов исследования является способ нулевой нагрузки: при отсутствии нагрузки усилия во всех стержнях статически определимой фермы должны иметь нулевые значения. Если же в каком-либо стержне усилия оказывается неопределенным, то ферма является изменяемой.
Для определения усилий в элементах статически определимых пространственных ферм применяют три основных способа:
1. Способ сечений;
2. Способ замены стержней;
3. Способ разложения на плоские фермы.
Способ сечений используется при определении усилий в фермах, имеющих простую схему образования, рассмотренную выше. Проводится сечение, пересекающее не более 6 стержней, и составляются уравнения равновесия одной из частей фермы. Различают три разновидности способа сечений:
· Способ моментов;
· Способ проекций;
· Способ вырезания узлов.
По сути, способ сечений для пространственных ферм не отличается от такого же способа для плоских ферм. Но пространственные задачи более сложны. Например, моменты необходимо вычислять не относительно моментной точки, а относительно моментной оси, т.е. такой оси, которую пересекают все усилия, кроме одного искомого. Ось проекций выбирается перпендикулярно не стержню, а плоскости, где расположены все стержни за исключением расчетного.
Способ замены стержней применяется для определения усилий в сложных пространственных системах, когда невозможно провести сечения, пересекающие не более 6 стержней. После замены одного или нескольких стержней сложная ферма превращается в простую. Усилие в заменяемом стержне обозначается x. Усилие в заменяющем стержне определяют по принципу суперпозиции: 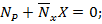
Где 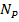 – усилие от нагрузки Р,
– усилие от нагрузки Р, 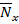 - усилие от
- усилие от 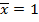 .
.
Решая уравнение, находят: 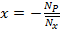
Способ разложения системы на плоские фермы применяется при рассмотрении пространственных ферм, у которых стержни группами располагаются в отдельных плоскостях, образуя несколько плоских ферм. При расчете таких ферм внешняя нагрузка раскладывается по направлениям плоских ферм и производится их расчет на эти составляющие.