
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В) Метод перемещений.
|
|
Степень кинематической неопределимости 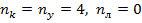 , т.к. в противном случае балка станет геометрически изменяема. Для выбора основной системы во всех опорных сечениях вводим виртуальные заделки.
, т.к. в противном случае балка станет геометрически изменяема. Для выбора основной системы во всех опорных сечениях вводим виртуальные заделки.
| ОснОсновная система метода перемещения |

Так как в каждом узле сходится два стержня и линейные перемещения отсутствуют, то для i промежуточной опоры каноническое уравнение упрощается к виду, аналогичному (*).
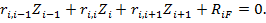
Оно носит название уравнения трех углов, т.к. все неизвестные играют роль углов поворота опорных сечений.
Для расчета неразрезных балок на временную нагрузку необходимо построение линий влияния. Однако для статически неопределимых балок такое построение становится затруднительным. Рассмотрим кинематический метод построения линий влияния, который позволяет легко получить форму линии влияния, но при этом не дает численных значений характерных ординат.
Сущность метода заключается в следующем:
1. Удаляется связь, соответствующая тому фактору, для которого строится линия влияния. Например, если строится линия влияния реакции, то нужно отбросить опору. Если строится линия влияния изгибающего момента в некотором сечении, то в этом сечении врезается шарнир. Если строится линия влияния поперечной силы, то производится так называемый скользящий разрез, когда расстояние межлу смежными сечениями при деформации балки не изменяется.
| брус |
| бр |
| ус |
| Шарнирное соединение (удалена одна горизонтальная связь) |
| Три внутренних связи Жесткое соединение 2 частей (склеивание) |
| Скользящий разрез (удалена одна диагональная связь) |
2. Удаленная связь заменяется соответствующей реакцией связи (согласно аксиоме статики) и составляется уравнение метода сил, выражающее равенство нулю перемешения по направлению отброшенной связи:
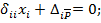
Где 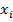 - искомое усилие,
- искомое усилие, 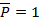 - единичная сила в произвольной точке балки,
- единичная сила в произвольной точке балки, 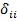 - возможное обобщенное перемещение по направлению
- возможное обобщенное перемещение по направлению 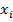 ; в качестве которого можно принять податливость основной системы,
; в качестве которого можно принять податливость основной системы, 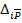 – перемещение по направлению
– перемещение по направлению 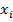 , вызванное единичной силой
, вызванное единичной силой 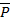 .
.
Согласно теореме Максвелла о взаимности перемещений 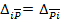 , где
, где  - перемещение по направлению единичной силы от действия искомого фактора
- перемещение по направлению единичной силы от действия искомого фактора 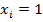 . Это перемещение полностью определяет вид упругой линии балки, т.е. эпюру прогибов.
. Это перемещение полностью определяет вид упругой линии балки, т.е. эпюру прогибов.
Решая каноническое уравнение, получаем:
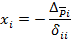
Таким образом, чтобы получить форму линии влияния, необходимо приложить к основной системе единичную силу 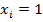 и показать примерный вид упругой линии балки.
и показать примерный вид упругой линии балки.
Построим линии влияния реакции 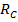 , изгибающего момента M1 и поперечной силы Q2.
, изгибающего момента M1 и поперечной силы Q2.
| Заданная система |
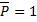 1 2
1 2
| A |
B 1 C 2 D E
RC
| Статически неопределимая основная система |
Опоры C нет
| Упругая линия балки = линия влияния RC |
| Кубическая парабола |
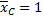
|

Шарнир
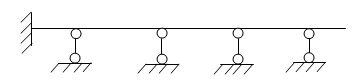
| Статически неопределимая основная система |
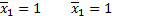

|
| Упругая линия балки = линия влияния М1 |

Скользящий разрез
| Статически неопределимая основная система |


| Упругая линия балки = линия влияния Q2 |

|
