Физическая сторона задачи.

Мы установили статические (1) и геометрические (2 а) зависимости. Для того, чтобы согласовать их между собой, воспользуемся законом Гука (какова деформация, такова сила, à какова сила, такова деформация).

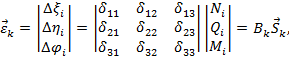
Где элементы 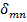матрицы 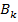есть абсолютные деформации по направлению m обобщенной силы, вызыванные действием единичной обобщенной силы в n направлении.

Рассмотрим схему стержня, эквивалентную заданной:

Q_i l_k F₂=Q_i

F₃=M_i

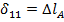
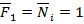
При действии продольной силы 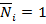стержень удлиняется на 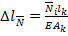, т.к.

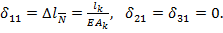
При действии поперечной силы 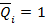стержень изгибается, образуя прогиб и угол поворота.

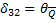
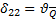
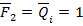
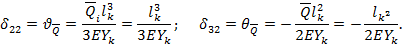
При действии изгибающего момента 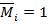стержень так же изгибается, образуя прогибы и угол поворота.

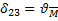
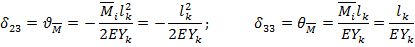
Матрица B_k принимает вид:

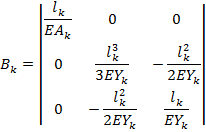
Закон Гука можно записать в прямой форме (какова деформация, такова сила):

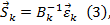где обратная матрица 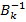имеет вид:

Подставим зависимость (3) и (2 а) в (1) (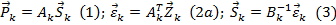) и получим:

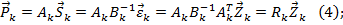
Где 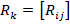- матрица жесткости для k стержня, имеющего узлы i, j. В развернутом виде матрицу жесткости стержня для случая α =0 (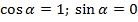) можно записать так:

Анализ отдельно взятого стержня закончен. Можно переходить к синтезу, т.е. к рассмотрению всей системы в целом. Исходные данные следующие:

1. Координаты узлов системы – геометрическая информация;

2. Жесткости поперечных сечений стержней – физическая информация;

3. Стержневая связь между узлами – топологическая информация;

4. Внешние нагрузки – статическая информация.

Требуется определить:

1. Усилия 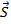во всех стрежнях;

2. Перемещения 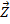всех узлов.

Обозначим: 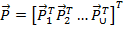– вектор узловых нагрузок системы;

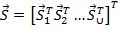- вектор внутренних усилий системы;

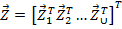- вектор узловых перемещений системы;

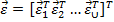- вектор абсолютных деформаций системы;

А – матрица равновесия системы;

В – матрица податливости системы;

R – матрица жесткости системы.

Для поставленной задачи имеем:

1. Уравнения равновесия

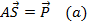
2. Геометрические уравнения

3. Физические зависимости закона Гука

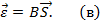
Так как в число неизвестных входят только усилия 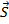и перемещения 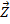, то исключим из трех видов уравнений вектор деформации 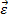. Подставим (а), (б), (в):

Объединим уравнения (а) и (г) в одну систему:

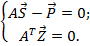(д)

Матрица А имеет 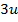строк и 3 S столбцов (u – число узлов, S – число стержней). Матрица 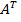имеет 3 S строк и 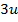столбцов.

Первое векторное уравнение содержит 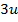алгебраических уравнений с 3 S неизвестными, а второе векторное уравнение - 3 S алгебраических уравнений с 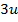неизвестными. Всего уравнений 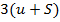; число неизвестных так же равно 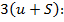каждый узел имеет 3 перемещения, а каждый стержень 3 усилия.

Выразим из второго векторного уравнения вектор усилий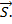

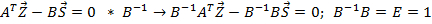
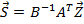
Подставим в первое векторное уравнение:

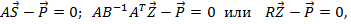
где 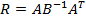- матрица жесткости системы.

Решая уравнение с 3 u неизвестными 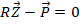находим перемещения всех узлов системы:

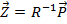
Затем вычисляем усилия во всех стержнях системы: