
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Смежный метод.
|
|
При выборе метода решения статически и кинематически неопределимых рам необходимо сравнить между собой число неизвестных по двум основным методам: сил и перемещений. Анализируя различные схемы рам, можно сделать общий вывод, что, если конструкция имеет малое количество лишних связей и большую линейную податливость, то выгодным является метод сил, а если конструкция имеет большое количество лишних связей и малую линейную податливость, то преимущество переходит к методу перемещений.
Р Р
а) б)
nл=3*6-2*8=2 nл=3*4-2*5-2=0
1 1
2 2 3
1 1 1
Для схемы (а) выгоден метод сил:
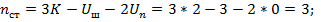
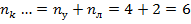
Для схемы (б) выгоден метод перемещений.
nст=3*3-0-2*2=5;
nk=1+0=1.
Встречаются конструкции, когда одна их часть имеет большое число лишних связей и малую податливость, а другая их часть, наоборот, имеет малое количество лишних связей и большую податливость. Для таких конструкций оказывается выгодным смешанный метод решения, когда в малоподатливой части за неизвестные принимают перемещения (углы поворота) Zi, а в сильно податливой части неизвестные принимают усилия Xj.
| х2 |
х1
| q |
| q |
Р
Z3 Z4
Заданная система Эквивалентная система смешанного метода
nст=3*3-2=7 nл=3*8-2*11=2
nk=4+2=6
nст-k=2+2=4 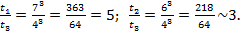
Первый этап рамы выгодно решать методом перемещений, а второй этап рамы – методом сил. Покажем эквивалентную систему смешанного метода где введены две виртуальные заделки в жесткие узлы и удалены две реальные связи в шарнирном узле. Таким образом при смешанном методе решения nст-k< 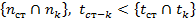 .
.
Система канонических уравнений смешанного метода запишется для данной рамы в следующем виде:
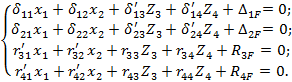
Здесь 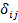 – перемещения по направлению отброшенных связей i, вызванные единичными силами
– перемещения по направлению отброшенных связей i, вызванные единичными силами 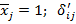 - перемещения по направлению отброшенных связей i, вызванные единичными перемещениями виртуальных связей
- перемещения по направлению отброшенных связей i, вызванные единичными перемещениями виртуальных связей 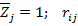 - реакции во введенных связях i, вызванные единичными перемещениями виртуальных связей
- реакции во введенных связях i, вызванные единичными перемещениями виртуальных связей 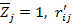 - реакции во введенных связях i, вызванные действием единичных сил по направлению отброшенных связей
- реакции во введенных связях i, вызванные действием единичных сил по направлению отброшенных связей 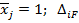 - перемещения по направлению отброшенных связей i от действия нагрузки
- перемещения по направлению отброшенных связей i от действия нагрузки 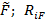 - реакции во введенных связях от действия внешней нагрузки
- реакции во введенных связях от действия внешней нагрузки 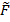 .
.
Податливости 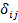 и реакции
и реакции 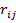 находят обычными приемами метода сил и метода перемещений. Реакции
находят обычными приемами метода сил и метода перемещений. Реакции 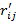 находят из единичных схем нагружения силами
находят из единичных схем нагружения силами 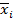 . Перемещения
. Перемещения 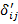 находят по теореме о взаимности реакций и перемещений:
находят по теореме о взаимности реакций и перемещений: 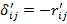 .
.
Перемещения 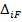 и реакции
и реакции 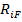 от внешних нагрузок находят обычными приемами двух методов.
от внешних нагрузок находят обычными приемами двух методов.
После решения системы канонических уравнений относительно 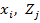 , строят окончательную эпюру изгибающих моментов:
, строят окончательную эпюру изгибающих моментов:
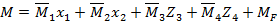 , где
, где 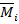 – единичные эпюры моментов в основной системе от действия
– единичные эпюры моментов в основной системе от действия 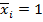 или
или 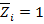 ,
, 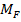 - грузовая эпюра моментов в основной системе от действия внешней нагрузки
- грузовая эпюра моментов в основной системе от действия внешней нагрузки 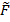 .
.