Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод сил
|
|
Основная проблема СНС – это наличие лишних связей, что наделяет эти системы особыми свойствами, рассмотренными выше. С точки зрения расчета, эти связи не позволяют решить задачу на основе уравнений равновесия и метода сечений. Необходимо, как известно, составить еще и n дополнительных уравнений на основе условий совместности деформаций (перемещений).
В методе сил за известное принимают реакции в лишних опорных связях и (или) внутренние усилия, соответствующие лишним внутренним связям. Эти неизвестные с целью упрощения разрешающих уравнений обозначают: 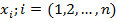 , где n=R-U – степень статической неопределимости, равная числу избыточных связей. Для плоских рам эта величина определяется по формуле:
, где n=R-U – степень статической неопределимости, равная числу избыточных связей. Для плоских рам эта величина определяется по формуле:
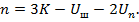
K- число замкнутых контуров;
Uш – число простых шарнирных узлов, включая шарнирно-неподвижные опоры;
Un – число подвижных узлов, включая шарниро-подвижные опоры (катки).
Из R внешних и внутренних связей необходимо выбрать n безусловно не необходимых и, отбросив их, получить основную систему, которая должна быть статически определимой и геометрически неизменяемой.
| x5 |
С
| x5 |
| x4 |
| x4 |
| IIk |
| P |
| Ik |
| Эквивалентная система |
| Основная система n0=R-U=3-3=0 |
| Заданная система n=3K-Uш-2Un=3*2-1-2*0=5. |
| A |
| MA |
| x2 |
| x3 |
Заданная рама 5 раз статически неопределима: 3 раза внешне и 2 раза внутренне. Наметим лишние связи: 3 внешних связи в заделке В и 2 внутренние связи в шарнире С. Показанная основная система геометрически неизменяема, т.к. состоит из одного диска, присоединенного к земле тремя связями. При этом она и статически определима. В эквивалентной системе введены следующие обозначения: x1=HB; x2=VB; x3=MB; x4=NC; x5=QC.
Так как мы заменили связи реакциями связей, то эквивалентная система полностью адекватна заданной системе как в статическом, так и в кинематическом смыслах (усилия и перемещения в заданной и эквивалентной системе одинаковы). Преимущество эквивалентной системы в том, что если силы x i причислить к внешним нагрузкам, то эквивалентная система статически определима и поэтому легко решается.
Вычислим перемещение по направлению i отброшенной связи, испльзуя принцип суперпозиции.
Для эквивалентрой системы:
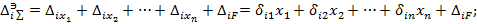
где 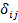 - податливость основной системы,
- податливость основной системы, 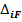 - перемещение вызванное заданной внешней нагрузкой в основной системе.
- перемещение вызванное заданной внешней нагрузкой в основной системе.
В заданной системе связи наложены, поэтому 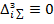 .
.
На основе адекватности 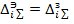 получаем:
получаем:
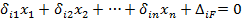 (
(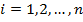 ).
).
Раскрывая по всем i, получаем систему канонических уравнений метода сил для определения лишних неизвестных:
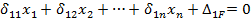
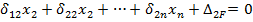
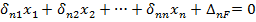
Каждое из уравнений имеет следующий физический смысл: перемещение в основной системе по направлению отброшенной связи, вызванное действием лишних неизвестных и внешней нагрузки, всегда равно нулю.
Податливости 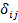 и перемещения
и перемещения 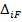 в основной системе определяют по интегралу Мора, с использованием правила Верещагина и формул трапеции или Симпсона.
в основной системе определяют по интегралу Мора, с использованием правила Верещагина и формул трапеции или Симпсона.
Например, чтобы определить податливость 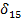 , рассмотренной нами необходимо построить и перемножить единичные эпюры
, рассмотренной нами необходимо построить и перемножить единичные эпюры 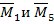 .
.
|
|

|
|

C1 C2
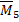
|
h h 

| 5 единичное состояние О.С. |
| 1 единичное состояние О.С. |
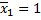
|
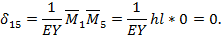
Горизонтальное перемещение т. В, вызванное действием сил 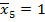 , равно нулю.
, равно нулю.
По теореме Максвелла о взаимности перемещений: 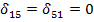 , т.е. взаимное перемещение по вертикали сечений С1 и С2, вызванное действием силы
, т.е. взаимное перемещение по вертикали сечений С1 и С2, вызванное действием силы 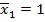 , равно нулю.
, равно нулю.
Чтобы определить перемещение ∆ 3F, необходимо построить и перемножить эпюры от сил 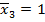 и
и 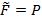 .
.
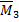
|
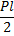
|
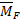
|
D
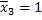
|
| Грузовое состояние О.С. |
| 3 единичное состояние О.С. |
1 1
Решая систему канонических уравнений, находят лишние неизвестные xi. Окончательную эпюру изгибающих моментов строят, используя принцип суперпозиции.
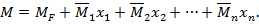
Для проверки правильности эпюры М используют статическую и кинематическую проверки. Статическая заключается в проверке равновесия всех узлов рамы, выделенных из конструкции и находящихся под действием изгибающих моментов в сходящихся стержнях и внешних моментов, приложенных в узлах. Например, для эпюры MF получаем для узла D:
0
D 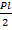
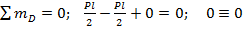 - узел D в равновесии.
- узел D в равновесии.
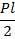
Кинематическая проверка заключается в отсутствии суммарных перемещений в заданной системе по направлению отбрасываемых связей:
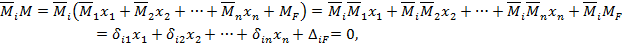
т.е. необходимо перемножить каждую из единичных эпюр 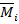 на окончательную эпюру М. Если ноль не получается, то допущена как минимум одна ошибка в расчетах (при первом расчете таких ошибок несколько). Для того, чтобы избежать неопределенности в нахождении ошибки, разработана система пошаговых промежуточных проверок.
на окончательную эпюру М. Если ноль не получается, то допущена как минимум одна ошибка в расчетах (при первом расчете таких ошибок несколько). Для того, чтобы избежать неопределенности в нахождении ошибки, разработана система пошаговых промежуточных проверок.
Эпюра поперечных сил Q для простых рам строится методом сечений. Для сходных рам эпюру Q строят путем вырезания отдельных стержней рамы с последующим рассмотрением их равновесия под действием внешних нагрузок и внутренних усилий по концам стержней. Так как нагрузки известны, изгибающие моменты можно принять с окончательной эпюры М, а продольные силы в составлении уравнений равновесия не участвуют, то можно вычислить поперечные силы по концам стержней.
Рассмотрим стержень ij:
y P q M
| Nij |
| Nij |
| b |
| a |
| l |
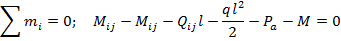
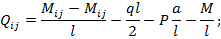
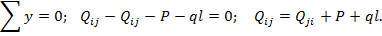
Эпюру продольных сил N для простой рамы можно построить методом сечений. Для схожей рамы эпюру N строят путем рассмотрения равновесия вырезанных узлов, находящихся под действием активных нагрузок поперечных сил, взятых с эпюры Q, и продольных сил. Необходимо последовательно рассматривать узлы, в которых неизвестными являются не более двух продольных сил. Например, для узла k получаем:
P1 Nkj j
P2 K Qkj
Qki
Nki
i
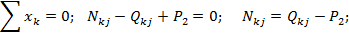
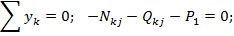
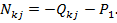
Для статической проверки всей рамы в целом необходимо приложить все опорные реакции и составить три уравнения равновесия, которые должны тождественно выполняться (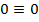 ):
):