Комбинированный метод.

Этот метод заключается в двукратном расчете статически неопределенной рамы:

1. Методом сил;

2. Методом перемещений с последующим суммированием полученных решений.

Не смотря на двойное решение задачи, общее время решения оказывается меньше, чем если бы задачу решали одним из методов. Комбинированный метод используется при расчете конструктивно симметричных рам, нагруженных произвольной нагрузкой. Раскроем секрет этого парадокса: t₁+t₂< t!

Рассмотрим конструктивно симметричную раму, нагруженную одной силой Р.

P ось симметрии

нагружение

A B A B A B

Вычислим степени статической и кинематической неопределимостей для двух методов.

1. Метод сил: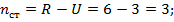

2. Метод перемещений: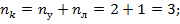

Время для решения задачи пропорционально третьей степени n, т.е.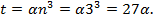

Представим силу Р в виде суммы симметричного и антисимметричного нагружения. При симметричном нагружении задачу выгодно решать методом перемещений, т.к.

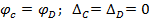, т.е. имеется только одна симметричная неизвестная Z₁ и для нее уравнение имеет вид: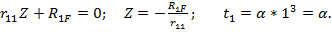

При антисимметричном нагружении задачу выгодно решать методом сил, т.к. если разрезать раму по оси симметрии, то N₀=0; M₀=0; 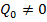, т.е. имеется только одна антисимметричная неизвестная х₁ и для нее уравнение имеет вид: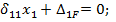

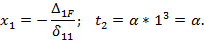
Складывая время, получаем: t₁+t₂=α +α =2α < < t=27α.

Время решения рассмотренных частных задач двумя методами на порядок меньше времени решения общей задачи любым из методов.