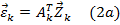Геометрическая сторона задачи.

Установим зависимость между перемещениями узлов i, j и абсолютными деформациями стрежня k. Введем базовый вектор абсолютной деформации:

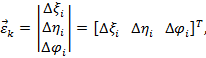
Где 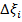- деформация, соответствующая продольной силе N_i (удлинение);

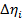- деформация, соответствующая поперечной силе Q_i (сдвиг);

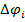– деформация, соответствующая изгибающему моменту M_i (поворот).

Базовый вектор перемещений узлов обозначим:

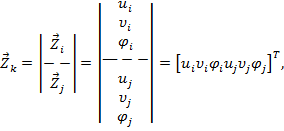
Где 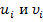- перемещения узлов по оси х, 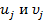- перемещения узлов по оси y, 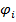и 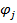- углы поворота узлов.

Если известны перемещения узлов, то через них можно выразить деформации. Эти геометрические соотношения более сложны при выводе, чем статические уравнения. В векторной форме эту зависимость можно представить по аналогии с зависимостью (1): 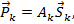т.е. 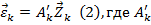- некоторая матрица преобразования.

Чтобы более просто установить вид этой матрицы, воспользуемся принципом Лагранжа: если механическая система находится в равновесии, то сумма работ внешних и внутренних сил равна нулю. В качестве возможных можно принимать действительные перемещения, если они достаточно малы.

Работа внешних сил совершается на перемещениях узлов, а работа внутренних усилий – на абсолютных деформациях. Работа внутренних сил на действительных деформациях всегда отрицательна, поэтому можно записать, учитывая, что стержень рассматривается в положении равновесия:

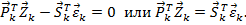
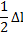
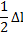
д

Подставляя в равенство формулы (1) и (2), получаем:

.

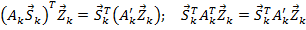Так как слева и справа стоят одинаковые вектора, то 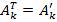или

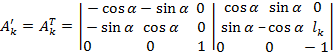
Таким образом,