
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод предельного равновесия.
|
|
Метод предельного равновесия называют так же методом разрушающих нагрузок, или методом расчета по несущей способности.
Условие прочности записывают в виде:
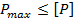 ,
,
Где 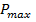 - наибольшая нагрузка, передаваемая на сооружение, а
- наибольшая нагрузка, передаваемая на сооружение, а 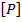 - допускаемая нагрузка, причем
- допускаемая нагрузка, причем 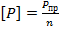 , где
, где 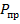 - предельная (разрушающая) нагрузка,
- предельная (разрушающая) нагрузка, 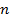 - коэффициент запаса прочности.
- коэффициент запаса прочности.
Для определения разрушающей нагрузки используется диаграмма Прандаля, представляющая собой упрощенную зависимость между напряжением 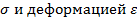 . Так ведет себя упругопластичный материал.
. Так ведет себя упругопластичный материал.
σ 
A B А
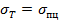
0 0 σ т
| ε T |
Так как деформация на площадке текучести АВ в сотни раз превышает деформацию в упругой зоне ОА, то используют так же еще более простую диаграмму для жестко-пластичного материала. Считается, что материал не деформируется до предела текучести, а затем ведет себя как пластичный.
Рассмотрим процесс развития пластических деформаций по высоте сечения изгибаемой балки.
| М h |
| М |
| 1 2 |
| 1 2 |
x My MT Myп∆ Mпр
| Работа в пластичной зоне |
| Работа в упруго-пластичной зоне |
| Работа на границе упругой и пласт. зон |
| Работа в упругой зоне |
b
Выразим изгибающий момент через предел текучести для случаев б) и г) для балки прямоугольного сечения.
Случай б) – материал работает на границе упругой и пластической зон, когда в крайних волокнах наблюдается фибровая текучесть.
Mt=σ TW,
Где 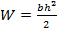 - осевой момент сопротивления.
- осевой момент сопротивления.
Случай г) – материал полностью находится в пластической зоне.
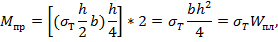
Где 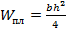 - пластический момент сопротивления сечения.
- пластический момент сопротивления сечения.
Сравнивая, находим 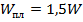 , следовательно, предельный момент Мпр в полтора раза превышает упругий момент М т, соответствующий фибровой текучести.
, следовательно, предельный момент Мпр в полтора раза превышает упругий момент М т, соответствующий фибровой текучести.
При возникновении во всех точках опасного сечения напряжений, равных пределу текучести, балка теряет несущую способность и становится геометрически изменяемой, так как ее части слева и справа от сечения могут поворачиваться друг относительно друга как при шарнирном сочленении. В таком случае говорят, что в сечении балки появился пластический шарнир.
Р
Аналогично теряет несущую способность любая статически определимая рама.
Статически неопределимая конструкция (рама) может превращаться в механизм, если в ее сечениях появится n+1 пластический шарнир, где n – степень статической неопределимости. Решение задачи усложняется тем, что заранее трудно предугадать места появления пластических шарниров.
При расчете сооружений по методу предельного равновесия необходимо придерживаться такой последовательности:
1. Предварительно проводят обычный упругий расчет, что позволяет установить убывающий ряд степени напряженности стержней сооружения, используя эпюру изгибающих моментов.
2. Показывают геометрически изменяемый механизм сооружения, вводя (n+1) пластический шарнир в наиболее напряженные сечения опасных стержней убывающего ряда.
3. Загружают геометрически изменяемую систему, имеющую одну степень свободы, предельными моментами Мпр в пластических шарнирах и предельными внешними нагрузками Рпр в заданных сечениях или узлах.
4. Составляют уравнение равновесия мезанизма, пользуясь принципом возможных перемещений. Находят предельную нагрузку.
Рассмотрим пример. Мпр
66, 14
h=3м
| 72, 27 |
| 21, 46 |
47, 73 ∆ 4
| М |
5 3
l=3м 30 53, 86
Мпр Мпр
Мпр
Мпр Мпр
Рама нагружена распределенной нагрузкой P=30кН/м и сосредоточенной силой Р=90кН. Рама 5 раз статически неопределима, если решать методом сил, и 2 раза кинематически неопределима если решать методом перемещений. Раскрыв неопределимость, получаем эпюру М. Для получения механизма с одной степенью свободы необходимо поставить 5+1=6 шарниров. Пронумеруем сечения по степени убывания моментов. Загружаем механизм предельными моментами и предельными внешними нагрузками.
Принимаем в качестве возможного перемещения угол поворота вертикальных стержней θ. Так как ригель не перемещается по вертикали, т.е. в направлении действия распределенной нагрузки, то она не совершает работы. Точка приложения сосредоточенной силы переместится по горизонтали на величину  . На этом перемещении сила совершает положительную работу Рпр∆; сечения 1-5 повернутся на угол θ, противоположный направлению моментов, следовательно, работа будет отрицательной.
. На этом перемещении сила совершает положительную работу Рпр∆; сечения 1-5 повернутся на угол θ, противоположный направлению моментов, следовательно, работа будет отрицательной.
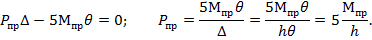
Рассмотрим стержень круглого сечения. Для него
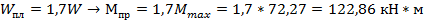
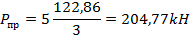
Чтобы получить допускаемую предельную нагрузку, разделим на коэффициент запаса прочности n=1, 5:
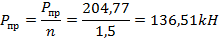
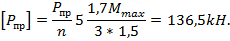
Условие прочности выполняется, т.к. 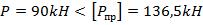
Экономия материала составит:
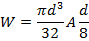
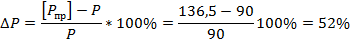
Момент сопротивления можно уменьшить на 52%.