
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формулы трапеций и Симпсона
|
|
Воспользуемся правилом Верещагина для перемножения двух прямолинейных эпюр, имеющих вид трапеций. Разобьем обе трапеции на треугольники, у которых площади и положения центров тяжести легко определяются.
Эпюра MF
ω 1
C1 C2 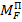
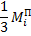
|
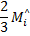
|
Эпюра 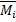
|
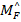 ω 2
ω 2
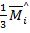
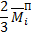
|
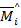
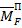
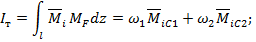
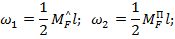
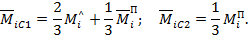
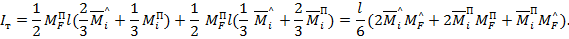
Мы получили формулу трапеций, согласно которой произведения соответствующих левых и правых ординат эпюр необходимо удвоить, а произведения перекрестных ординат взять одинарными, и полученную сумму умножить на одну шестую длины эпюр.
Рассмотрим случай, когда грузовая эпюра представлена квадратной параболой, а единичная эпюра – трапецией.
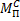
|
| Наряду с крайними ординатами укажем и средние. Разобьем криволинейную эпюру на трапецию и параболический сегмент. Произведем перемножение соответствующих фигур. |
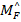
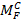
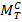
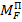
ω T
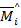
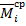
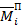
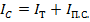
Выражение IТ у нас имеется. Найдем 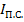 .
.
Площадь параболического сегмента:
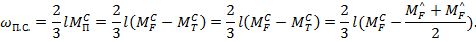
Ордината единичной эпюры под центром тяжести параболического сегмента:
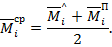
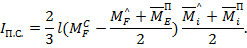
После подстановки получаем формулу Симпсона:
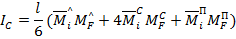
Произведение двух эпюр равно сумме произведений крайних ординат и учетверенному произведению средних ординат, умноженной на одну шестую длины эпюр.