Интеграл Мора для определения перемещений

Перемещение любой точки конструкции есть суммарная интегральная функция от произведения внутренних усилий, возникающих в сечениях в двух состояниях системы: действительном и возможном.

i P_i=1

i

Для изгибаемых конструкций интеграл Мора имеет вид:

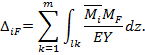
При доказательстве теоремы Бетти мы рассмотрели две последовательности нарущения упругой конструкции и получили:

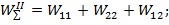
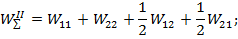
при этом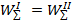

Следовательно, можно записать равенство:

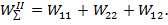
Выразим отсюда взаимную работу:

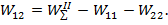
Работы, стоящие в правой части, заменим потенциальными энергиями внутренних усилий (моментов), учитывая, что M(F₁, F₂)=M(F₁)+M(F₂)=M₁+M₂.

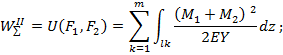
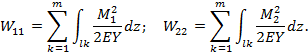
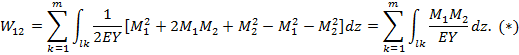
Взаимная работа выражается через обобщенную силу и обобщенное перемещение.

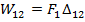
Применим в качестве I обобщенной силы возможную (отсутствующую в реальном времени) единичную силу .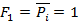

В качестве II обобщенной силы принимаем заданные внешние нагрузки 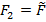. Следовательно, ∆ ₁₂ – это действительное перемещение от внешних нагрузок по направлению возможной единичной силы:

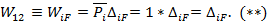
Приравнивая правые части формул (*) и (**), получаем:

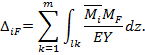
Эта формула носит название интеграла Мора для определения перемещений.

Здесь ∆ _iF – действительное перемещение i точки конструкции в направлении единичной обобщенной силы, вызванное внешней нагрузкой; 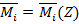и изгибающий момент, возникающий в сечении Z от действия единичной силы 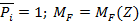- изгибающий момент, возникающий в сечении Z от действия заданной внешней нагрузки .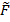