
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Бетти
|
|
Работа сил первого состояния (I группа сил) на перемещениях по их направлению, вызванных силами второго состояния (II группа сил), равна работе сил второго состояния на перемещениях по их направлению, вызванных силами первого состояния:
W12=W21
Рассмотрим две последовательности нагружения упругой конструкции двумя обобщенными силами F1 и F2.
Первая последовательность: статически прикладываем I силу F1 , статически прикладываем II силу F2 .
Вторая последовательность: прикладываем статически обе силы одновременно (F1, F2) .
A F1 B ∆ 21 A1 B F2
∆ 11 A1 B1 F F1 ∆ 1Σ ∆ 2Σ
F1 A2 ∆ 12 B2 A2 B2
∆ 11 – действительное перемещение по направлению I силы от действия этой же силы; ∆ 22 – то же для II направления, ∆ 12 – возможное перемещение по направлению I силы, вызванное действием второй силы, ∆ 21 – то же для II направления.
∆ iΣ – перемещение по направлению I силы от действия двух сил одновременно, ∆ 2Σ – то же для II направления.
Вычислим суммарную работу для обеих последовательностей нагружения:
WΣ I= 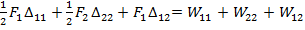
W11, W22, W12 – действительная работа;
WΣ II= 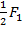 ∆ 1Σ
∆ 1Σ 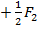 ∆ 2Σ
∆ 2Σ 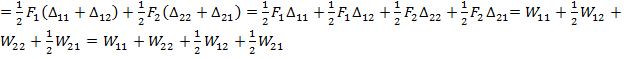 .
.
Согласно принципу произвольной очередности нарушения:
WΣ I = WΣ II или W11+W22+W12 = W11+W22+ 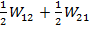 .
.