Теорема о потенциальной энергии внутренних сил упругости

Потенциальная энергия есть суммарная интегральная квадратичная функция внутренних усилий, возникающих во всех сечениях элементов сооружения при его нагружении.

Для пространственных конструкций она имеет следующее выражение:

1 слагаемое учитывает растяжение-сжатие;

2 и 3 слагаемые учитывают сдвиг;

4 и 5 слагаемые учитывают изгиб;

6 слагаемое учитывает кручение.

Для плоских стержневых систем:

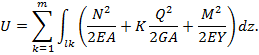
Для плоских рам, стержни которых работают преимущественно на изгиб:

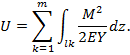
Докажем последнюю формулу. Выделим из стержня (балки), подверженного чистому изгибу, элемент бесконечно малой длины и рассмотрим схему его деформации, вызванной действием изгибающих моментов, переведенных в разряд внешних сил.

dθ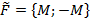

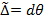
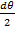
M M

dz

Примем оба момента М за обобщенную силу, а взаимный элементарный угол поворота смежных сечений 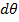за обобщенное перемещение. Тогда, согласно теореме Клапейрона, элементарная работа будет равна: .

Воспользуемся дифференциальным уравнением изогнутой оси балки:

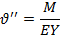
Преобразуем его, учитывая что .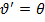

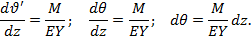
Подставляя в элементарную работу, получаем:

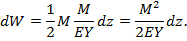
Интегрируя по всей длине стержня, находим:

Согласно закону сохранения энергии работа, совершаемая внешними силами, с небольшими потерями (порядка 0, 01%) на нагрев и другие эффекты переходит в потенциальную энергию внутренних сил упругости. Эта энергия, накаливаясь в элементах сооружения, обеспечивает его равновесное состояние при воздействии нагрузок и возвращает в исходное состояние после снятия нагрузок. Произведем суммирование по всем m стержням сооружения и учтем, что U=W. Тогда получаем:

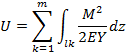
Мы видим, что изгибающий момент стоит под знаком интеграла во второй степени и, следовательно, потенциальная энергия внутренних сил упругости есть интегральная квадратичная функция внутреннего усилия. В силу этого к потенциальной энергии не применим принцип суперпозиции, т.е. если обозначать энергию, создаваемую при действии силы F₁ через U_1, создаваемую при действии силы F₂ через U₂, создаваемую при действии обеих сил через U, то 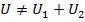, в общем случае U_Σ .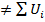