
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод расчета страховых запасов
|
|
Для гарантированного исключения потерь, появляющихся в результате нарушения поставок или возникновения непредвиденного спроса, создаются страховые (резервные) заделы. Чем больше вероятность сбоев, тем больше должен быть размер страховых запасов. Однако хранение резерва сопряжено с определенными затратами. Для оптимизации размера страховых запасов необходимо учитывать эти противоположные тенденции. Рассмотрим один из возможных подходов, позволяющий разрешить эти противоречия.
Предположим, что пополнение запасов производится регулярно. Интервал между двумя последовательными поставками примем за единицу времени. Потребность в ресурсах в единицу времени будем считать случайной величиной, принимающей значения a + b и a - b с равной вероятностью 0, 5. Очевидно, что a есть средняя потребность в ресурсах за единицу времени, а b — стандартное отклонение потребности за тот же период времени. Размер поставки считаем равным средней потребности a. Через r обозначим страховой запас. Принимаем 0 < r < b (ибо при r³ b дефицит отсутствует). Использование запасов в обоих случаях показано на рис. 18.7. Очевидно, что
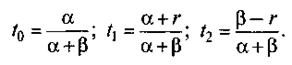 (18.2)
(18.2)
Отметим, что издержки содержания текущих запасов во внимание не принимаются, ибо они не зависят от r. В случае, представленном на рис. 18.7, а, издержки содержания страховых запасов выражаются как
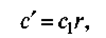 (18.3)
(18.3)
а в случае, представленном на рис. 18.7, б, эти затраты в интервале t1 имеют вид:
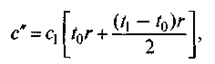 (18.4)
(18.4)
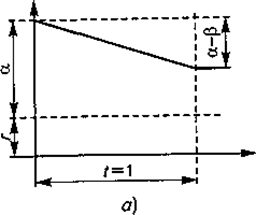 где c1 - издержки, связанные с содержанием единицы страхового запаса в единицу времени.
где c1 - издержки, связанные с содержанием единицы страхового запаса в единицу времени.
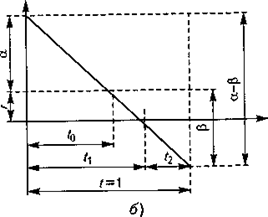
Рис. 18.7. Использование запаса:
а - при потребности a - b, б - при потребностии a + b
Итак, издержки содержания страховых запасов представляют собой случайную величину, принимающую значения, которые рассчитываются по формулам (18.3) - (18.4), с равной вероятностью 0, 5. Следовательно, среднее значение издержек хранения резервов с учетом формулы (18.2) составит:
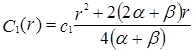 (18.5)
(18.5)
Потери от дефицита есть случайная величина, принимающая значение нуль (см. рис. 18.7, а) и 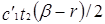 (см. рис. 18.7, б) также с вероятностью 0, 5, где с1' - потери от дефицита, приходящиеся на единицу недостающих запасов в единицу времени. Таким образом, среднее значение потерь от дефицита с учетом формулы (18.2) равно:
(см. рис. 18.7, б) также с вероятностью 0, 5, где с1' - потери от дефицита, приходящиеся на единицу недостающих запасов в единицу времени. Таким образом, среднее значение потерь от дефицита с учетом формулы (18.2) равно:
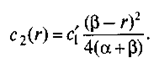 (18.6)
(18.6)
В качес тве критерия принимаем среднее значение суммарных затрат:
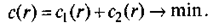
Из выражений (18.5) и (18.6) имеем:
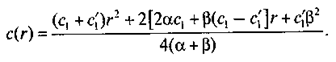
Для определения минимального значения этой функции находим ее производную и приравниваем ее нулю:
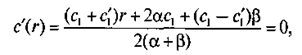
откуда легко определить оптимальный страховой запас:
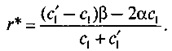
Очевидно, что r* > 0, когда выполняется неравенство:
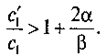
В противном случае функция возрастает на всем интервале (0, b) и, следовательно, r* = 0.
Контрольные вопросы и задания
1. Назовите системы управления запасами и дайте их характеристику.
2. Постройте многопродуктовую модель управления запасами готовой продукции и дайте экономическую интерпретацию параметров модели.
3. определите издержки для одного воспроизводимого фактора, если заданы органичения на капитал.
4. Как вы относитеь к тезису: «Самый маленький склад – самый лучший»?
5. Какие показатели необходимоучитывать при расчете оптимального размера страхового запаса?
6. Ежедневный расход расточных резцов на предприятии находится в пределах от 60 до 80 шт., принимая на этом интервале с равной вероятностью любое значение. Инструментальный цех пополняет запас резцов ритмично. Требуется найти ритм поставки резцов, максимальную и минимальную партии поставки, резервный запас, если известно, что на складе может храниться одновременно не более 680 шт. рассчитать величину текущей партии поставки, если заказ делается за 2 дня до ее получения, когда на складе по данным учета осталось 230 резцов, а интенсивность их потребления ожидается на уровне 69 шт. в день.
7. Ежедневный расход электродов для электросварки со склада строительной фирмы находится в пределах 180 до 320 шт., изменяясь по равномерному закону. Поставщик пополняет запас электродов партиями по 2600 шт. Срок поставки – 6 дней. Требуется рассчитать точку заказа, резервный запас и максимальное чило электродов, которое может одновременно находиться на складе.
8. Ежедневно магазин продает от 78 до 141 кг вареной колбасы. Емкость холодильника, где она хранится, - 960 кг, а минимальная партия поставки колбасы с завода – 600 кг в ассортименте. Требуется определить максимально допустимый для магазина при этих условиях срок поставки колбасы с мясоперерабатывающего комбината (в днях). Оценить возможность дозагрузки холодильников другой продукцией. Рассчитать точку заказа, резервный запас колбасы. Учесть, что срок реализации продукта не должен превышать 10 дней.
9. Определить емкость склада сырья на предприятии, оптимальный размер партии его поставки, точку заказа, резервный запас, если по договору с поставщиком срок поставки очередной партии составляет 3 дня, а затраты на поставку - 400 руб. За год предприятие потребляет 90 000 т сырья, среднегодовые затраты на хранение 1 т на складе - 22 руб. Интенсивность потребления сырья — величина случайная, нормально распределенная с параметрами MI = 500 т/дн. и sI = 20 т/дн. По условиям производства дефицит сырья на предприятии допустим с вероятностью 6%, а переполнение склада должно быть исключено с вероятностью 90%.
10. Склад сборочного цеха рассчитан на хранение 18 360 корпусов прибора. Корпуса поступают из цеха-изготовителя партиями по 13 000 шт. Срок поставки очередной партии с равной вероятностью может принимать значения от 4до 12 рабочих дней. Интенсивность ежедневной подачи корпусов на сборку - величина случайная, нормально распределенная с параметрами МI = 620шт./дн.; sI = 45, 3 шт./дн. Требуется определить вероятность возникновения простоев сборочной линии из-за нехватки корпусов и вероятность переполнения ими склада, если точка заказа установлена на уровне 7800 корпусов.