
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение линий пересечения поверхностей способом вспомогательных сфер
|
|
Для построения линии пересечения поверхностей вместо вспомогательных секущих плоскостей при определенных условиях удобно применять вспомогательные сферические поверхности.
В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеетпреимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции пересекающихся поверхностей (рис. 216).
Вспомогательные сферические поверхности построения линий пересечения поверхностей можно применять лишь при следующих условиях:
а) пересекающиеся поверхности должны быть поверхностями вращения;
б) оси поверхностей вращения должны пересекаться; точка пересечения осей является центром вспомогательных сфер;
в) оси поверхностей вращения должны быть
параллельны какой-либо плоскости проекций.
Примеры применения вспомогательных сферических поверхностей показаны на рис. 216, а и б.
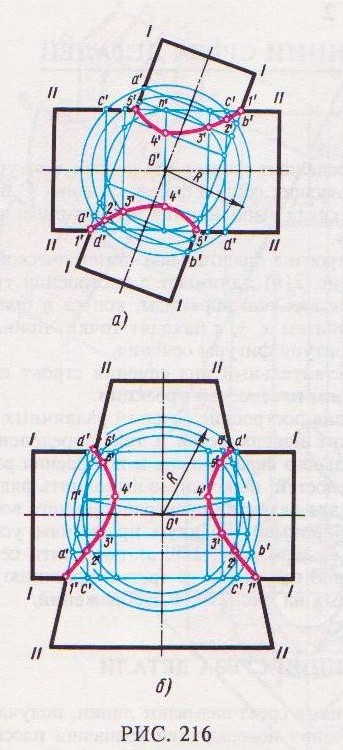
На рис. 216, а дано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.
Вспомогательные сферические поверхности проводят из точки О' пересечения осей цилиндров.
Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О' проводят сферически, ю поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса. Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и BD, а наклонно расположенный цилиндр – по окружностям диаметра АВ.
В пересечении полученных проекций окружнос-
тей – отрезков а'b' и c'd' – находят проекцию 2' промежуточной точки линии пересечения.
Вводя еще целый ряд вспомогательных сферических поверхностей, можно построить необходимое число точек линии пересечения.
Пределы радиусов сферических поверхностей находят следующим образом (рис. 216, а и б): наибольшая окружность сферической поверхности должна пересекаться с контурными образующими I–I и II–II цилиндра и наименьшая должна быть касательной к одной из данных пересекающихся поверхностей и пересекаться с образующими другой поверхности.
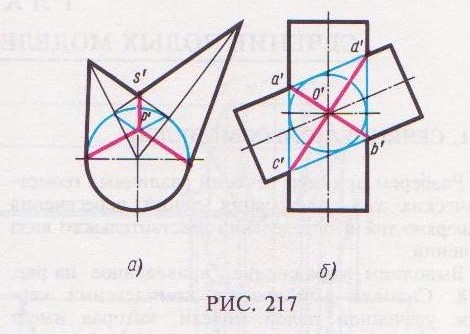
Если поверхности двух конусов (рис. 217, а) описаны около шара, то они касаются шара по двум окружностям; эти окружности пересекаются в двух точках, которые проецируются на фронтальную плоскость проекций в точку р'. Плоскости, в которых лежат эти окружности, пересекаются по прямой, соединяющей точки пересечения линий касания конусов с шаром. Окружности проецируются на фронтальную плоскость проекций в виде прямых линий.
Соединив очевидную точку s' пересечения конусов с точкой р', получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.
Разберем второй подобный пример. Если два прямых круговых цилиндра с осями, пересекающимися в точке О' (рис. 217, б), описаны около шара с центром в точке О, то фронтальная проекция шара будет окружностью, касательной к контурным образующим цилиндров. Линии пересечения поверхностей этих цилиндров представляют собой эллипсы, фронтальные проекции которых изображаются в виде прямых линий а'b' и c'd'.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ ___________________
1. Что называется линией перехода?
2. Как строится линия пересечения поверхностей?
3. В чем заключается принцип решения задач на взаимное пересечение поверхностей?