Методы интегрирования уравнения движения поезда.

Все практические вопросы тяги поездов: определение массы состава, скоростей движения, времени прохождения отдельных перегонов, решение тормозных задач, определение расхода электроэнергии и топлива решаются при помощи уравнения движения поезда.

В 1898 г. появились графические способы интегрирования уравнения движения поезда. В России был опубликован способ Шведе, а во Франции способ Дедуи, однако оба эти способа не получили широкого практического применения.

Значительно большее применение получил графический способ, предложенный группой русских инженеров, работавших в конторе опытов при Министерстве путей сообщения России (способ МПС).

Графоаналитические способы расчёта скорости и времени хода поезда были предложены Васютынским (1903 г.), Чечоттом (1910 г.). Способ интегрирования уравнения движения поезда с разложением в ряды был предложен Н.Н. Дегтеревым (1919 г.), разработавшим в дальнейшем и несколько графических способов.

Кратко рассмотрим некоторые способы решения уравнения движения поезда, используемые на практике до сих пор.

2.3.1. Графический метод. Графический метод основан на принципе конечных приращений и геометрической связи диаграммы равнодействующей сил f _y = ¦(V) с интегральной кривой V = ¦(s), существующей благодаря общей зависимости силы f _y и пути от скорости.

Графический метод дает сравнительно невысокую точность расчетов и требует больших затрат времени. В настоящее время этот метод утратил свое значение в связи с развитием электронно-вычислительных машин (ЭВМ).

2.3.2. Аналитический метод. Запишем уравнение движения поезда, развернув его правую часть:

,

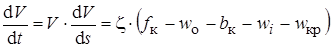где f _к и b _к – соответственно удельная сила тяги и торможения;

w _о, w_i, w _кр – удельное сопротивление движению, соответственно основное, от уклонов, кривых.

Из анализа приведенного выражения следует, что уравнение движения поезда возможно интегрировать по:

- пути;

- скорости;

- времени.

Для реализации этих возможностей необходимо иметь аналитические зависимости всех входящих в уравнение движения составляющих, причем, зависимости необходимо иметь от той переменной, по которой производится интегрирование.

Из всех составляющих уравнения движения только для основного сопротивления движению существуют аналитические зависимости в функции скорости (w _о = f (V)). Для механического колодочного торможения существуют аналитические зависимости коэффициента трения от скорости движения, поэтому получить зависимость b _к = f (V) также нетрудно.

Тяговые, а так же тормозные характеристики электрического торможения большинства типов ЭПС, как правило, представлены в графическом или табличном виде в функции скорости. Для использования этих характеристик при аналитическом методе решения уравнения движения необходимо преобразовать их в аналитические выражения, что нетрудно сделать с использованием современных математических компьютерных пакетов.

Зависимость сопротивления движению от уклонов представлена в функции пути. Зависимость сопротивления движению от кривых может быть представлена одновременно в функции пути и скорости:

где R _кр – радиус кривой;

t_к – непогашенное ускорение в кривой.

,

где h – возвышение наружного рельса в кривой;

S _к – расстояние между кругами катания колес;

g – ускорение свободного падения.

Наиболее простая и наглядная формула получается при отсутствии возвышения наружного рельса:

.

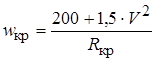Получить зависимости сопротивления движению от уклонов и кривых в функции скорости возможно только в том случае, если уже имеется зависимость скорости от пути.

Из сказанного выше следует сделать вывод, что решение уравнения движения поезда аналитическим методом в чистом виде практически не встречается.

Для практических задач используются менее точные методы, сущность которых сводится к замене дифференциалов конечными приращениями. Уравнение движения в этом случае приобретает вид:

.

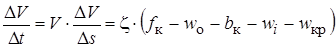Величины, входящие в правую часть уравнения на каждом шаге расчета принимаются постоянными – то есть производится кусочно-линейная аппроксимация интегральных кривых. Проанализируем, какую из переменных наиболее рационально принимать за независимую.

В случае использования в качестве независимой переменной скорости расчет на каждом шаге производится в следующем порядке: D V_i ® D t_i ® D s_i.

;

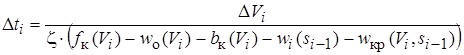D s_i = V _{ср i} × D t_i.

Здесь V _{ср i} – средняя скорость движения на i -м шаге расчета:

.

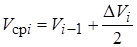Из выражения для приращения времени следует, что величины сопротивления движению от уклонов и кривых " запаздывают" на один шаг расчета вследствие того, что нам еще неизвестна координата поезда на данном шаге расчета. Это приводит к некоторой погрешности вычислений. Кроме этого, данный метод неприменим при установившемся режиме движения (f _у ® 0 Þ D t ® ¥).

В случае использования в качестве независимой переменной времени расчет на каждом шаге производится в следующем порядке: D t_i ® D V_i ® D s_i.

D V_i = D t_i × z × (f _к(V_{i -1}) – w _o(V_{i -1}) – b _к(V_{i -1}) – w_i (s_{i -1}) – w _кр(V_{i -1}, s_{i -1}));

D s_i = V _{ср i} × D t_i.

В данном случае " запаздывают" все составляющие удельной равнодействующей силы, но нет проблем с установившимся режимом движения.

В случае использования в качестве независимой переменной пути расчет на каждом шаге производится в следующем порядке: D s_i ® D V_i ® D t_i.

;

.

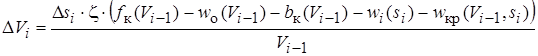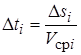Как следует из приведенных выше выражений, наименьшую погрешность должно дать интегрирование уравнения движения по скорости. Однако этот способ не позволяет интегрировать уравнение при установившемся режиме движения. Для исключения значительных погрешностей вычислений при подходе к установившемуся режиму движения (вследствие больших приращений пройденного пути возможен " пропуск" элементов профиля) следует, во-первых, уменьшать шаг интегрирования, и, во-вторых – при попадании величины удельной равнодействующей силы в некоторый диапазон f _{у min} £ f _у £ f _{у max} следует считать режим движения установившимся. Величина диапазона выбирается исходя из требуемой точности расчетов.

При моделировании пуска или электрического торможения электропоездов с контакторно-реостатной системой регулирования удобно интегрирование уравнения движения по току тягового двигателя (косвенное интегрирование по скорости). При этом

,

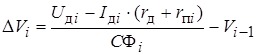где U _{д i} – напряжение, прикладываемое к тяговому двигателю на i -м шаге;

I _дi × (r_д + r_{п i} ) – падение напряжения на активном сопротивлении обмоток тягового двигателя и пускового резистора;

С ф _i – магнитный поток, соответствующий току I _{д i} .

Использование тока тягового двигателя в качестве независимой переменной при интегрировании уравнения движения поезда имеет еще одно преимущество перед остальными способами – возможность уменьшения памяти ЭВМ, необходимой для хранения тяговых и тормозных характеристик ЭПС и уменьшения предварительной работы по обработке характеристик и вводу их в ЭВМ.

Поскольку решение уравнения движения поезда, как правило, подразумевает выбор оптимального с точки зрения расхода электроэнергии режима движения поезда, то необходимо иметь два семейства характеристик – тяговые (тормозные) и токовые. Как известно, сила тяги на ободе колеса определяется выражением

F _к = С Ф_к× I _д,

скорость движения

.

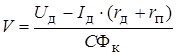В оба выражения входит величина нагрузочной характеристики тягового электродвигателя С Ф_к, приведенной к ободу колеса. Следовательно, оба семейства характеристик можно описать, имея зависимость С Ф_к = ¦(I _в). В этом случае объем требуемой памяти ЭВМ и объем предварительных вычислений уменьшается как минимум вдвое. Для вычислений на ЭВМ зависимость С Ф_к = ¦(I _в) целесообразно представить в виде степенного полинома вида

.

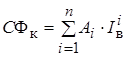Коэффициенты полинома А_i нетрудно получить с использованием одного из математических компьютерных пакетов. Степень полинома n выбирается исходя из требуемой точности вычислений.

Таким образом, в режимах тяги и электрического торможения уравнение движения поезда для практических задач целесообразно интегрировать по току тягового электродвигателя; в режимах выбега и механического торможения – по скорости. При подходе к установившемуся режиму шаг интегрирования следует уменьшать. Критерием выбора величины шага интегрирования может быть точность расчетов, например допустимая погрешность прицельного торможения у остановочного пункта или длина элемента профиля. В установившихся режимах интегрировать уравнение движения следует по времени или пути.

2.3.3. Численные методы. Сущность их заключается в замене нелинейного дифференциального уравнения движения поезда линейным дифференциальным, решение которого с достаточной для практики точностью приближается к решению нелинейного уравнения, то есть в линеаризации уравнения движения поезда. Основным допущением, позволяющим производить линеаризацию, является принцип малых отклонений входящих в уравнение переменных от тех значений, которые приняты в качестве исходных для линеаризации.

Известно много различных методов численного интегрирования дифференциальных уравнений: Чаплыгина, Адамса, Рунге-Кутта, Милна и других. Эти методы обеспечивают сравнительно высокую степень точности, но требуют большого объема подготовительных работ. В тяговых расчетах используют менее точные, но более простые – метод Эйлера и разложения кривой v = f (t) в ряд Тейлора.

Метод Эйлера. Запишем уравнение движения поезда в виде:

.

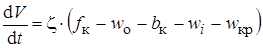Выражение для удельной равнодействующей силы заменим некоторой функцией j, которая зависит от скорости и времени:

.

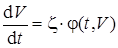Интегрирование уравнения движения методом Эйлера ведется по времени. Интервал времени, на котором решается уравнение разделим на n равных частей:

.

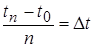Дифференциалы на каждом шаге расчета заменяем конечными приращениями. С учетом того, что правую часть уравнения на каждом шаге считаем постоянной, для i -го шага имеем:

D V_i = z× j _{i -1}× D t.

То есть искомая кривая v (t) на каждом шаге заменяется касательной линией, проведенной в точке, соответствующей началу шага.

Скорость движения и координата на i -м шаге:

V_i = V_{i -1} + D V_i;

.

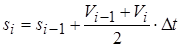Таким образом, сущность метода Эйлера сводится к аппроксимации интегральной кривой v (t) последовательно сопряженными касательными, проведенными в точках, соответствующих началу каждого шага.

Решение уравнения движения поезда разложением в ряд Тейлора. Как известно, функцию вида y = f (x) можно разложить в ряд Тейлора:

,

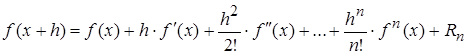где h – приращение независимой переменной;

R_n – остаточный член ряда.

Предположим, что в результате решения уравнения движения поезда необходимо получить зависимость скорости движения от времени. За независимую переменную примем время. В этом случае для i -го шага расчета имеем:

f (x) = V_{i -1}; h = D t;

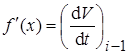– тангенс угла наклона кривой скорости к оси времени в точке, соответствующей началу шага i;

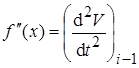– тангенс угла наклона кривой ускорения к оси времени в точке, соответствующей началу шага i.

Тогда

.

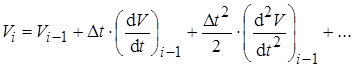Приращение пути вычисляется аналогично методу Эйлера.

В случае использования такой величины приращения времени, чтобы D V_i £ 0, 1 км/ч, для расчетов можно ограничиться только первыми двумя членами ряда Тейлора:

.

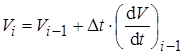При этом уравнение движения поезда решается аналогично методу Эйлера.