Особенности движения поездов повышенной массы и длины.

Во первых, следует определиться в терминах:

- поездом повышенной массы, согласно ПТЭ следует считать поезд, масса которого превышает графиковую не менее, чем на 100 т;

- поездом повышенной длины следует считать поезд, длина которого, в условных вагонах, больше графиковой;

- тяжеловесным поездом следует считать поезд, масса которого превышает 6 тыс.т.;

- длинносоставным поездом следует считать поезд, который имеет в своем составе более 350 осей.

Исходя из этих определений, тяжеловесный поезд может не быть длинносоставным и наоборот.

Рассмотрим случай движения длинносоставного поезда на переломистом профиле с постоянной скоростью. Предположим, что поезд расположен на трех элементах профиля: головная и хвостовая часть – на подъеме, а средняя часть – на спуске.

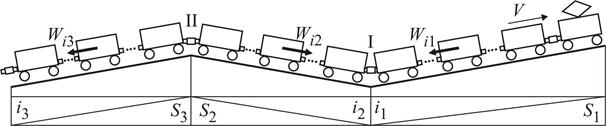
Головная и хвостовая части поезда, под действием сил W_{i 1} и W_{i 3}стремятся замедлиться; а средняя часть – ускориться под действием силы W_{i 2}. За счет зазоров в автосцепных приборах и их упругих элементов вагоны в поезде могут перемещаться относительно друг друга (в поезде длиной 2, 5 км сумма зазоров в автосцепках может достигать 10 м). Следовательно, средняя часть поезда набегает на головную и в зоне I появляется угроза выдавливания вагонов; а в зоне II – опасность обрыва поезда. При изменении режима движения (разгон или торможение) возникает дополнительная сила, которая в одних частях поезда усиливает действие сил W_i, в других – ослабляет их.

Рассмотрим, какие изменения необходимо внести в уравнение движения поезда для учета воздействий от переломистого профиля. Предположим, что поезд массой М, длиной L находится на n элементах профиля, имеющих уклоны соответственно i ₁, i ₂, …, i_n и длины s ₁, s ₂, …, s_n. Поезд состоит из вагонов различных типов с различной загрузкой, т.е. он имеет неоднородное распределение массы по длине m = ¦(x).

Для начала рассмотрим один элемент профиля с номером k. В произвольный момент времени на выбранном элементе профиля находится часть поезда, массой m_k. На нее действует сила сопротивления движению от уклона

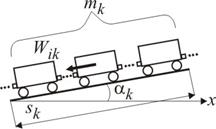W_ik = m_k × g × sina _k.

За элементарный промежуток времени d t происходит изменение силы сопротивления движению от уклона на d W_ik за счет того, что масса поезда, находящаяся на выбранном элементе профиля изменилась на d m_k. Очевидно, что за время прохождения поездом этого элемента сила сопротивления движению будет равна:

.

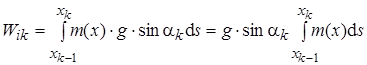Для удобства интегрирования необходимо произвести замену d s на d x. Вообще-то проекция d s на горизонтальную ось х равна d s × cosa _k, но так как величина a _k мала (при максимальном уклоне, допустимом на магистральных железных дорогах 25‰ a = 1, 4°), то можно считать d x» d s.

Переходя к поезду в целом можно записать:

.

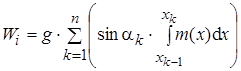Уравнение движения поезда в этом случае будет иметь вид

.

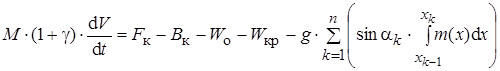Переходя к более привычным удельным величинам, имеем:

.

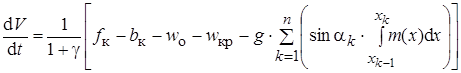В том случае, если масса поезда равномерно распределена по его длине формула, существенно упрощается:

.

.
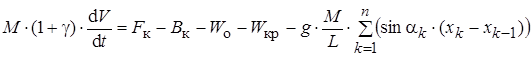
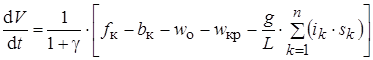