Закон распределения дискретной случайной величины. Случайные величины, их виды

Глава II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайные величины, их виды

В математике величина – это общее название различных количественных характеристик предметов и явлений. Длина, площадь, температура, давление и т.д. – примеры разных величин.

Величина, которая принимает различные числовые значения под влиянием случайных обстоятельств, называется случайной величиной. Примеры случайных величин: число больных на приеме у врача; точные размеры внутренних органов людей и т.д.

Различаютдискретные инепрерывные случайные величины.

Случайная величина называется дискретной, если она принимает только определенные отделенные друг от друга значения, которые можно установить и перечислить.

Примерами дискретной случайной величиной являются:

– число студентов в аудитории – может быть только целым положительным числом: 0, 1, 2, 3, 4….. 20…..;

– цифра, которая появляется на верхней грани при бросании игральной кости – может принимать лишь целые значения от 1 до 6;

– относительная частота попадания в цель при 10 выстрелах – ее значения: 0; 0, 1; 0, 2; 0, 3 …1

– число событий, происходящих за одинаковые промежутки времени: частота пульса, число вызовов скорой помощи за час, количество операций в месяц с летальным исходом и т.д.

Случайная величина называется непрерывной, если она может принимать любые значения внутри определенного интервала, который иногда имеет резко выраженные границы, а иногда – нет *. К непрерывным случайным величинам относятся, например, масса тела и рост взрослых людей, масса тела и объем мозга, количественное содержание ферментов у здоровых людей, размеры форменных элементов крови, р Н крови и т.п.

Понятие случайной величины играет определяющую роль в современной теории вероятностей, разработавшей специальные приемы перехода от случайных событий к случайным величинам.

Если случайная величина зависит от времени, то можно говорить о случайном процессе.

Закон распределения дискретной случайной величины

Чтобы дать полную характеристику дискретной случайной величины необходимо указать все ее возможные значения и их вероятности.

Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом распределения этой величины.

Обозначим возможные значения случайной величины Х через х_i, а соответствующие им вероятности – через р_i *. Тогда закон распределения дискретной случайной величины можно задать тремя способами: в виде таблицы, графика или формулы.

В таблице, которая называется рядом распределения, перечисляются все возможные значения дискретной случайной величины Х и соответствующие этим значениям вероятности Р (Х):

При этом сумма всех вероятностей р_i должна быть равна единице (условие нормировки):

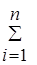р_i = p₁ + p₂ +... + p_n = 1. (13)

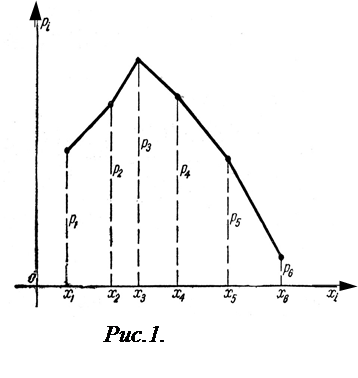Графически закон представляется ломаной линией, которую принято называть многоугольником распределения(рис.1). Здесь по горизонтальной оси откладывают все возможные значения случайной величины х_i, , а по вертикальной оси – соответствующие им вероятности р_i

Аналитически закон выражается формулой. Например, если вероятность попадания в цель при одном выстреле равна р, то вероятность поражения цели 1 раз при n выстрелах дается формулой Р (n) = n q^n-1× p, где q = 1 – р – вероятность промаха при одном выстреле.