
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон распределения непрерывной случайной величины. Плотность распределения вероятности
|
|
Для непрерывных случайных величин невозможно применить закон распределения в формах, приведенных выше, поскольку такая величина имеет бесчисленное («несчетное») множество возможных значений, сплошь заполняющих некоторый интервал. Поэтому составить таблицу, в которой были бы перечислены все ее возможные значения, или построить многоугольник распределения нельзя. Кроме того, вероятность какого-либо ее конкретного значения очень мала (близка к 0)*. Вместе с тем различные области (интервалы) возможных значений непрерывной случайной величины не равновероятны. Таким образом, и в данном случае действует некий закон распределения, хотя и не в прежнем смысле.
Рассмотрим непрерывную случайную величину Х, возможные значения которой сплошь заполняют некий интервал (а, b)**. Закон распределения вероятностей такой величины должен позволить найти вероятность попадания ее значения в любой заданный интервал (х1, х2), лежащий внутри (а, b), рис.2.
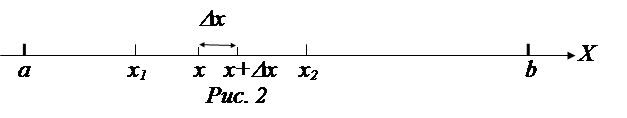
Эту вероятность обозначают Р (х1 < Х < х2), или
Р (х1 £ Х £ х2).
Рассмотрим сначала оченьмалый интервал значений Х – от х до (х + Dх); см. рис.2. Малая вероятность dР того, что случайная величина Х примет какое-то значение из интервала (х, х + Dх), будет пропорциональна величине данного интервала Dх: dР ~ Dх, или, введя коэффициент пропорциональности f, который сам может зависеть от х, получим:
dР = f (х) × D х = f (x) × dx (14)
Введенная здесь функция f (х) называется плотностью распределения вероятностей случайной величины Х, или, короче, плотностью вероятности, плотностью распределения. Уравнение (13) – дифференциальное уравнение, решение которого дает вероятность попадания величины Х в интервал (х1, х2):
Р (х1 < Х < х2) =  f (х) dх. (15)
f (х) dх. (15)
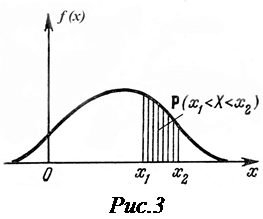
Графически вероятность Р (х1 < Х < х2) равна площади криволинейной трапеции, ограниченной осью абсцисс, кривой f (х) и прямыми Х = х1 и Х = х2 (рис.3). Это следует из геометрического смысла определенного интеграла (15) Кривая f (х) при этом называется кривой распределения.
Из (15) следует, что если известна функция f (х), то, изменяя пределы интегрирования, можно найти вероятность для любых интересующих нас интервалов. Поэтому именно задание функции f (х)полностью определяет закон распределения для непрерывных случайных величин.
 Для плотности вероятности f (х) должно выполняться условие нормировкив виде:
Для плотности вероятности f (х) должно выполняться условие нормировкив виде:
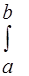 f (х) dх = 1, (16)
f (х) dх = 1, (16)
если известно, что все значения Х лежат в интервале (а, b), или в виде:
 f (х) dх = 1, (17)
f (х) dх = 1, (17)
если границы интервала для значений Х точно неопределенны. Условия нормировкиплотности вероятности (16) или (17) являются следствием того, что значения случайной величины Х достоверно лежат в пределах (а, b) или (-¥, +¥). Из (16) и (17) следует, что площадь фигуры, ограниченной кривой распределения и осью абсцисс, всегда равна 1.