Основные числовые характеристики случайных величин

Результаты, изложенные в параграфах 2.2 и 2.3, показывают, что полную характеристикудискретной и непрерывной случайных величин можно получить, зная законы их распределения. Однако во многих практически значимых ситуациях пользуются так называемымичисловыми характеристиками случайных величин, главное назначение этих характеристик – выразить в сжатой форме наиболее существенные особенности распределения случайных величин. Важно, что данные параметры представляют собой конкретные (постоянные) значения, которые можно оценивать с помощью полученных в опытах данных. Этими оценками занимается «Описательная статистика».

В теории вероятностей и математической статистике используется достаточно много различных характеристик, но мы рассмотрим только наиболее употребляемые. Причем лишь для части из них приведем формулы, по которым рассчитываются их значения, в остальных случаях вычисления оставим компьютеру.

Рассмотрим характеристики положения – математическое ожидание, моду, медиану.

Онихарактеризуют положение случайной величины на числовой оси, т.е.указывают некоторое ориентировочное значение, около которого группируются все возможные значения случайной величины. Среди них важнейшую роль играет математическое ожидание М (Х).

Математическое ожидание М (Х) случайной величины Х является вероятностным аналогом ее среднего арифметического 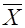(М (Х) = 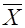или М (Х)» ).

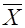Для дискретной случайной величины М (Х) вычисляется по формуле:

М (Х) = х₁р₁ + х₂р₂ +…+ х_nр_n = 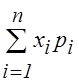. (18)

Для непрерывной случайной величины М (Х) определяют по формулам:

М (Х) = 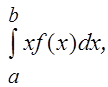или М (Х) = 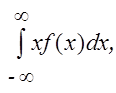(19)

где f (x) – плотность вероятности, dP = f (x) dx – элемент вероятности (аналог p_i для малого интервала D x (dx)).

Пример: Вычислите среднее значение непрерывной случайной величины, имеющей на отрезке (a, b) равномерное распределение.

Решение: при равномерном распределении плотность вероятности на интервале (a, b) постоянна, т.е. f (х) = f_o = const, а вне (a, b) равна нулю; из условия нормировки (15) найдем значение f₀:

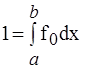= f₀ = f₀ × x 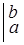= (b-a) f₀, откуда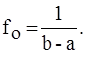

Поэтому:

M (X) = 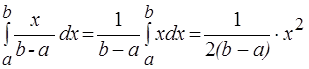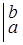= = 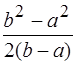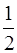(a + b).

Следовательно, математическое ожидание М(Х) совпадает с серединой интервала (a, b), определяющей 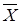, т.е. 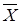= M (X) = .

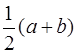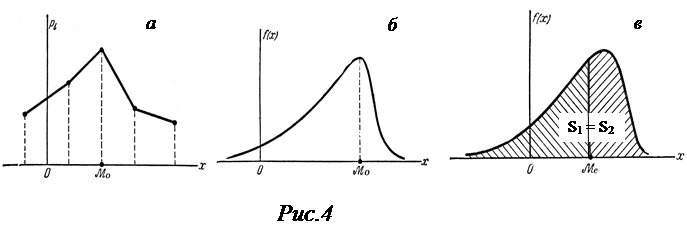
Модой Мо (Х) дискретной случайной величины называют ее наиболее вероятное значение (рис. 4 а), а непрерывной – значение Х, при котором плотность вероятности максимальна (рис.4 б).

Медианой (Ме) случайной величины обычно пользуются только для непрерывных случайных величин, хотя формально ее можно определить и для дискретных Х. Медианой Ме (Х)случайной величины называют такое значение Х, которое делит все распределение на две равновероятные части, т.е. вероятности Р (Х < Ме) и Р (Х > Ме) оказываются равными между собой:

Р (Х < Ме) = Р (Х > Ме) = .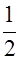

Поэтому медиану можно вычислить из соотношения:

= .

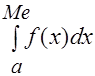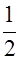Графически медиана – это значение случайной величины, ордината которой делит площадь, ограниченную кривой распределения, пополам: S ₁ = S ₂ (рис. 4 в).

Если М (Х), Мо (Х) и Ме (Х) совпадают, то распределение случайной величины называют симметричным, в противном случае – асимметричным.

Характеристики рассеяния – это дисперсия и стандартное отклонение (среднее квадратическое отклонение)

Дисперсия D (X)случайной величины Х определяется как математическое ожидание квадрата отклонения случайной Х от ее математического ожидания М (Х):

D (X) = M [ X – M (X)] ², (20)

или D (X) = M (X² ) – [ M (X)] ² . (21)

При конкретных расчетах для дискретной случайной величины эти формулы записываются так:

D (X) = 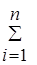[ х_i–М (Х)] ² × р_i, или D (X) = 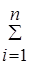х_i² р_i – [ M (X)] ² (22)

Для непрерывной случайной величины, распределенной в интервале (a, b), они имеют вид:

D (X) = 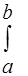[ x–M (X)] ² f (x) dx, или D (X) = 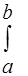х² f (x) dx – [ M (X)] ², (23)

а для интервала (-∞, +∞):

D (X) = 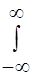[ x–M (X)] ² f (x) dx, или D (X) = 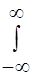х² f (x) dx– [ M (X)] ². (24)

Дисперсия характеризует рассеяние, разбросанность, значений случайной величины Х относительно ее математического ожидания. Само слово «дисперсия» означает «рассеяние».

Однако дисперсия D (Х) имеет размерность квадрата случайной величины, что весьма неудобно при оценке разброса в физических, биологических, медицинских и других приложениях. Поэтому обычно пользуются параметром, размерность которого совпадает с размерностью Х. Это – среднее квадратическое (иначе – стандартное) отклонение случайной величины Х, которое обозначают s (Х):

s (Х) = 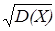. (25)

Итак, математическое ожидание, мода, медиана, дисперсия и среднее квадратическое отклонение являются наиболее употребляемыми числовыми характеристиками случайных величин, каждая из которых выражает какое-нибудь характерное свойство их распределения.