Пример 1. На рис.3. - таблица «Численность постоянного населения в среднем за год, млн

На рис.3. - таблица «Численность постоянного населения в среднем за год, млн. человек, г.Санкт-Петербург, значение показателя за год» приведена в интервале A3: B23. Требуется проверить наличие аномальных наблюдений.

На рис.4. приведен график динамики временного ряда. Визуально подозрительными на аномальность выглядят значения временного ряда пр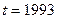и и 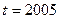, поскольку этим наблюдениям соответствуют резкие выбросы.

.

Рис.3. Динамика временного ряда. «Численность постоянного населения в среднем за год, млн. человек, г.Санкт-Петербург, значение показателя за год» режим отображения данных.

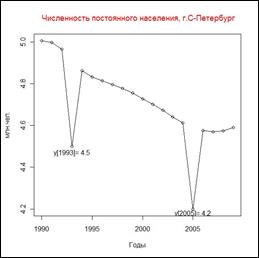
Рис.4. График динамики временного ряда. «Численность постоянного населения в среднем за год, млн. человек, г.Санкт-Петербург, значение показателя за год» исходные данные.

Результаты расчетов по методу Ирвина приведены на рис.3. Среднее значение 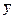и стандартное отклонение 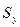уровней динамического ряда приведены в интервале A25: B26, при этом 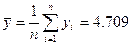и .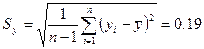

Расчетные значения 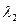, 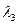и т.д. приведены в интервале С5: С23. Критическое значение критерия Ирвина при n=20 и уровне значимости α равном 0.05 найдем в Приложении 1, 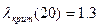. Аномальными являются наблюдения 1993 и 2005, поскольку и 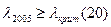. Эти выбросы заменены соответствующими значениями равными среднему значению двух соседних значений. Расчеты приведены на рис.3. и рис.6. в интервале D5: D23; на рис.5 приведен график динамики исправленного временного ряда.

Рис.5. График динамики временного ряда. «Численность постоянного населения в среднем за год, млн. человек, г.Санкт-Петербург, значение показателя за год» исправленные данные.

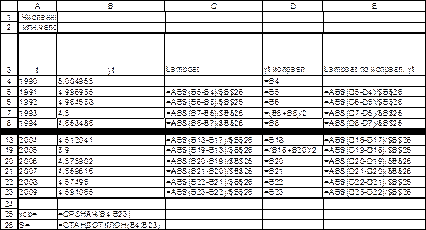
Рис.6. Динамика временного ряда. «Численность постоянного населения в среднем за год, млн. человек, г.Санкт-Петербург, значение показателя за год» режим отображения формул.

Определение наличия тренда

Для определения " наличия - отсутствия " тренда в исходном временном ряду применяют ряд методов: критерий серий (основан на медиане выборки), метод проверки разностей средних уровней и другие.

Критерий серий, основанный на медиане. Проверка с помощью этого критерия сводится к проведению следующей последовательности шагов:

1) Вычисление медианы. Это можно сделать с помощью встроенной функции MS Excel

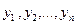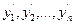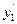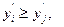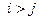· Из исходного ряда длиной n образуется ранжированный ряд , где - наименьшее значение и если (т.е. 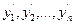ряд из значений исходного ряда, упорядоченных по возрастанию).

· Определяется медиана Me(y) вариационного ряда. Если n нечетное (n=2m+1), то 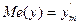, в противоположном случае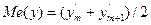

2) Формирование последовательности 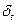по правилу:

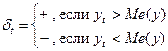
(5)

Если значение 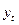равно медиане 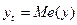, то это значение пропускается;

3) Определение 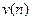– числа серий в совокупности 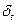, где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или один минус тоже считается серией.

Определение 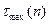протяженности самой длинной серии.

4) Проверка гипотезы основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий – слишком маленьким. Поэтому для того, чтобы не была отвергнута гипотеза о случайности исходного ряда (об отсутствии систематической составляющей, т.е. тренда) необходимо выполнение следующих неравенств (для 5% уровня значимости)

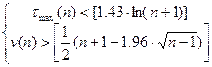
(6)

Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии тренда отвергается. Квадратные скобки в правой части неравенства означают вычисление целой части числа. Целая часть числа А – [A] – это целое число, ближайшее к А и не превосходящее А.

Метод проверки разностей средних уровней. Основная идея этого метода сравнение средних значений двух частей временного ряда. Если эти средние совпадают или не очень сильно отличаются, то тенденция в исходном ряде отсутствует, в противном случае тенденции есть. Проверка равенства средних значений осуществляется с помощью критерия Стьюдента. Реализация этого метода состоит из 4-х этапов:

- на 1-м этапе исходный временной ряд 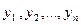разбивается на две, примерно равные по числу уровней, част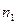и: и 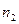, при этом ;

­ на 2-м этапе для каждой из частей вычисляются средние значения и дисперсии:

; ;

;

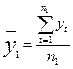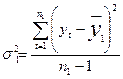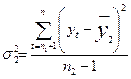
3-й этап заключается в проверке равенства дисперсий обеих частей с помощью F-критерия Фишера:

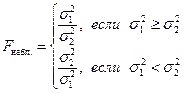
(7)

По заданному уровню значимости α и числам степеней свободы 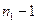и 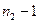определяем 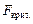по таблицам или используя встроенные функции MS Excel.

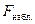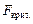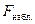
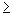
Если расчетное значение меньше , то делается вывод, что следует применить критерий Стьюдента с равными дисперсиями и переходят к 4-му этапу. Если 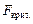то делается вывод, что следует применить критерий Стьюдента с различными дисперсиями [9].

На 4-м этапе определяется расчетное значение критерия Стьюдента по формуле:

,

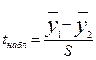(8)

где

.

Если 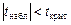с заданным уровнем значимости α, то тренда нет, в противном случае тренд есть.

Сглаживание временных рядов

Сглаживание временного ряда, состоит в замене фактических уровней ряда расчетными значениями, которые имеют меньшую колеблемость, чем исходные данные. Соответствующее преобразование называется фильтрованием.

Сглаживание временных рядов проводится по следующим причинам:

· Для выявления тенденции. Часто графическое изображение сглаженных значений временного ряда позволяет проследить тренд более четко.

· Для устранения аномальных наблюдений.

· Для непосредственного анализа и прогнозирования экономических показателей.

Сглаживания временных рядов можно осуществлять аналитическими или механическими методами.

Суть механических методов сглаживания заключается в следующем: берется несколько первых уровней временного ряда, образующих интервал сглаживания, и для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженное значение и т.д.

Суть аналитических методов заключается в построении функции, график которой проходит между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний. Методы аналитического сглаживания рассмотрены ниже.

Для механического сглаживания временных рядов часто используются следующие методы:

· укрупнение временных интервалов;

· простой скользящей средней;

· взвешенной скользящей средней;

· экспоненциального сглаживания.

Простейшим методом механического сглаживания является укрупнение временных интервалов. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев рассчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.