Пример 4. Стержневая система, показанная на рис

Стержневая система, показанная на рис. а, вращается с постоянной угловой скоростью 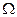вокруг оси АВС. Построить эпюру изгибающих моментов М_и от действия инерционных сил и определить допустимое по прочности число оборотов в минуту, если плотность материала стержней = 7, 75 г/см³, а допускаемое нормальное напряжение R_adm =160 МПа. Поперечные сечения стержней круглые диаметром d = 3 см, длина отрезка а = 0, 2 м.

Решение.

Определяем интенсивность сил инерции р_i в отдельных стержнях.

Участок АВС. Силы инерции отдельных частиц стержня взаимно уравновешиваются и изгиба не вызывают; таким образом р_i^АВС = 0;

Участок СD. Силы инерции направлены вдоль оси стержня. На расстоянии x от оси вращения интенсивность их будет равна

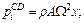
т.е. при x = 0 имеем 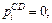а при x = а получаем 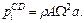Обозначим буквой q интенсивность сил инерции в точке х = а, т.е.

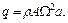
Участок DЕ. Так как этот участок параллелен оси вращения, то интенсивность сил инерции на нем будет постоянна и равна

р_i^DE = q = const.

Эпюры инерционных сил, действующих на рассматриваемую систему, показаны на рис. б.

Далее определяем изгибающие моменты и строим эпюру М_и. На участке DE эпюра М_и – парабола, на участке DC – прямая, параллельная стержню CD, на участке СB – наклонная прямая и на участке АВ также наклонная прямая (рис. в).

У к а з а н и е. Равнодействующая распределенной вдоль стержня CD инерционной нагрузки p_i равна площади эпюры p_i, т.е. в данном случае площади треугольника (R = aq /2).

Из эпюры М_и видно, что максимальное значение изгибающего момента будет в сечении В

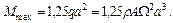
Запишем условие прочности в виде 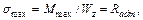где осевой момент сопротивления круглого поперечного сечения подсчитываем по формуле W_z = 0, 1 d ³.

Таким образом, условие прочности имеет вид

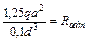или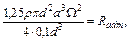

откуда находим допускаемую угловую скорость в рад/сек

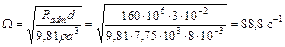
и допускаемое число оборотов в минуту