Решение. Чтобы определить динамический коэффициент по формуле , необходимо найти прогиб точки С (точки приложения нагрузки Q) от статического действия нагрузки

Чтобы определить динамический коэффициент по формуле 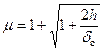, необходимо найти прогиб 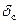точки С (точки приложения нагрузки Q) от статического действия нагрузки. Найдем этот прогиб, используя метод Максвелла–Мора и интегрируя формулу Максвелла–Мора с помощью правила Верещагина. Для этого построим эпюры изгибающих моментов от нагрузки Q (рис. 2, а) и от единичной силы, соответствующей искомому перемещению (рис. 2, б). Перемножим эти эпюры по правилу Верещагина:

.

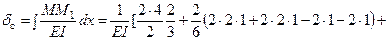
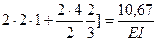Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в " см"

Рис.2

.

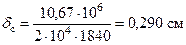Найдем динамический коэффициент по формуле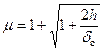

.

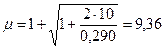Определим максимальные нормальные напряжения в опасном сечении от статического действия нагрузки. В рассматриваемом примере несколько равно опасных сечений с изгибающим моментом 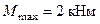. Максимальные статические напряжения равны

.

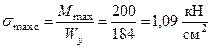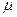Динамические напряжения от действия ударной нагрузки увеличатся согласно формуле в раз.

.

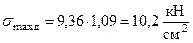Видно, что динамические напряжения не превосходят предела пропорциональности 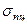= 200 МПа, и материал работает упруго.

Во столько же раз увеличится и динамический прогиб:

.
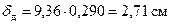