Решение. 1. Раскрытие статической неопредимости рамы

1. Раскрытие статической неопредимости рамы

Выбираем эквивалентную систему, отбрасывая реакцию катка и заменяя ее неизвестной силой X₁ (рис. 2, а).

а) построение грузовой эпюры

Определяем реакцию заделки A, проецируя все внешние силы на ось y (рис. 2, б):

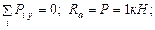
Изгибающий момент от статической силы P на 2 участке будет:

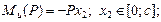
в сечении D момент равен 0, в сечении A:

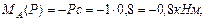
Строим эпюру моментов от силы P (рис. 2, в).

б) построение эпюры моментов от единичной силы

Вместо неизвестной X₁ прикладываем единичную силу 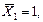и рассматриваем ее действие на раму (рис. 2, г). Реакция заделки в этом случае равна:

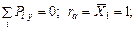
Изгибающий момент от единичной силы равен:

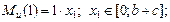
в сечении C момент равен 0, в сечении A:

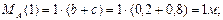
Строим эпюру моментов от единичной силы (рис.2, д).

в) решение канонического уравнения

В сечении B приложения неизвестной реакции прогиб равен 0 (т.к. катковая опора препятствует вертикальному перемещению), поэтому и в сечении C прогиб равен 0, т.е. суммарный прогиб от действия неизвестной реакции X₁ и силы P равен 0:

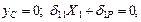
где 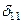, 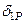– прогибы от действия единичной силы и силы P.

Находим прогибы способом Верещагина:

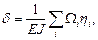
где 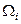– площадь фигуры на грузовой эпюре, 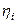– ордината под центром тяжести этой фигуры на эпюре единичной силы.

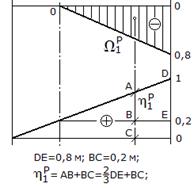
Рис.3

Находим прогиб от единичной силы: площадью фигуры в формуле Верещагина будет площадь эпюры единичной силы, ординатой – ордината под центром тяжести эпюры единичной силы (2/3 высоты эпюры); поэтому:

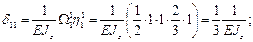
Находим прогиб от силы P: площадью фигуры будет площадь грузовой эпюры, ординатой – ордината на эпюре единичной силы под центром тяжести грузовой эпюры (рис. 3); поэтому:

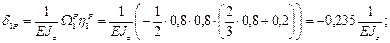
Тогда, решая каноническое уравнение получаем:

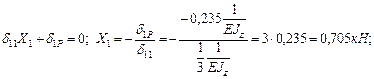
Неизвестная реакция X₁ равна по величине и направлена по направлению единичной силы.

2. Определение статического прогиба и динамического коэффициента

а) построение эпюры изгибающих моментов

Определяем реакцию заделки A с учетом реакции отброшенной опоры (рис. 2, е):

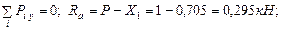
Изгибающий момент на 1 участке равен:

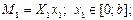
в сечении C момент равен 0, в сечении D:

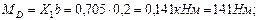
Изгибающий момент на 2 участке:

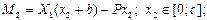
в сечении А момент равен:

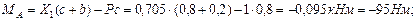
Строим эпюру изгибающих моментов (рис. 2, ж).

б) построение эпюры единичной силы

В сечении D прикладываем единичную силу и рассматриваем ее действие на раму (рис. 2, з). Момент от единичной силы возникает только на 2 участке рамы:

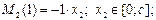
в сечении D момент равен 0, в сечении A:

Строим эпюру изгибающего момента от единичной силы (рис. 2, и).

в) определение статического прогиба

Определяем статический прогиб с помощью интеграла Мора:

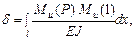
где M_и(P), M_и(1) – изгибающие моменты, возникающие под действием силы P и единичной силы.

В данном случае:

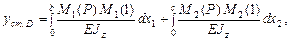
но т.к. на 1 участке единичная сила момента не создает, то первое слагаемое обращается в ноль:

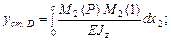
с учетом моментов, создаваемых силой P и единичной силой на 2 участке получаем:

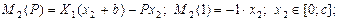
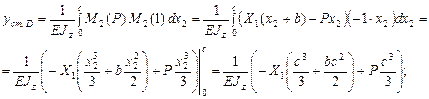
Учитывая, что сечение рамы круглое, находим его момент инерции:

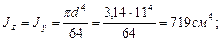
тогда статический прогиб равен:

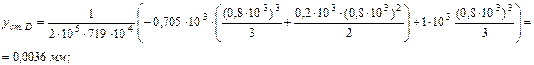
Вычисляем динамический коэффициент по приближенной формуле:

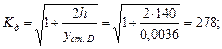
3. Определение динамических напряжений и прогибов

Динамические напряжения определяются как:

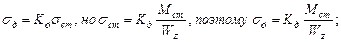
Учитывая, что сечение рамы круглое, находим его момент сопротивления:

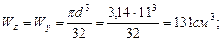
Считая статический изгибающий момент максимальным, действующим в сечениях рамы, находим максимальные динамические напряжения:

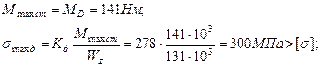
Таким образом, максимальные динамические напряжения превышают допустимые напряжения 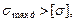подбираем новое сечение рамы, исходя из условия прочности:

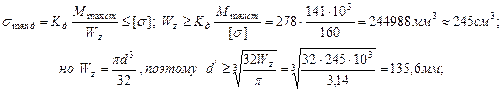
Округляем диаметр нового сечения рамы до стандартного 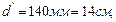выбранного из ряда Ra 40 нормальных линейных размеров (ГОСТ 6636–69), тогда для нового сечения:

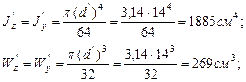
Максимальные динамические напряжения, возникающие в раме с новым сечением:

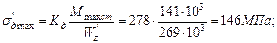
Определяем статический прогиб для рамы с новым сечением:

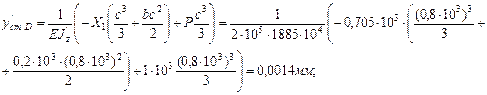
Пересчитываем динамический коэффициент:

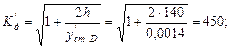
Динамический прогиб в сечении падения груза будет: