
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взнос на амортизацию единицы.
|
|
Эта функция позволяет определить аннуитетные платежи в погашение текущей стоимости объекта или кредита:
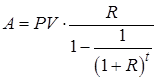 . (16)
. (16)
При использовании эффективной ставки процента формула (16) примет, соответственно, вид:
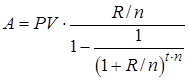 . (17)
. (17)
Пример 8:
На приобретение квартиры выдан кредит в размере 200 тыс руб. сроком на 5 лет под 15 % годовых. Выплаты по кредиту осуществляются аннуитетным методом в конце каждого года. Определить, какую сумму должна выплачивать семья ежегодно в погашение кредита.
Решение:
Дано:
PV=4 00; R= 0, 15; t= 5
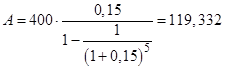 тыс. руб.
тыс. руб.
Пример 9:
На приобретение квартиры выдан кредит в размере 400 тыс руб. сроком на 5 лет под 15 % годовых. Выплаты по кредиту осуществляются аннуитетным методом в конце каждого месяца. Определить, какую сумму должна выплачивать семья ежемесячно в погашение кредита.
Решение:
Дано:
PV=4 00; R= 0, 15; t= 5; n = 12
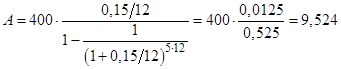 тыс. руб.
тыс. руб.
В примере 9 можно видеть, что общая сумма выплат по кредиту при ежемесячном погашении будет значительно меньше, чем в случае ежегодного погашения, рассмотренного в примере 8 (9, 524× 12× 5 = 571, 44, что меньше суммы выплат 119, 32× 5 = 571, 44).