
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение оптимизационных задач
|
|
Большинство задач в строительном материаловедении и технологии, как и в любой практической деятельности, предполагает выбор решения из множества возможных вариантов. Оптимизация - определение наиболее целесообразного варианта решения, т. е. лучшего с точки зрения намеченной цели. Сравнение вариантов по отношению к цели осуществляется на основе критерия предпочтения - критерия оптимальности(эффективности, качества и др.).
В строительно-технологической практике содержание задач оптимизации может быть самым разным: организовывать поставку сырьевых материалов заводу железобетонных конструкций и вывоз готовых изделий таким образом, чтобы транспортные расходы были минимальны; обеспечить как можно более низкий процент брака при назначении параметров технологического процесса; снизить расход портландцемента при производстве изделий требуемого качества за счет использования добавок и наполнителей; определить соотношение между компонентами полимерной композиции, обеспечивающее максимальную прочность материала при изгибе, и т. д.
Решить содержательно разные задачи оптимизации позволяют общие математические методы. Для этого необходимо конкретную задачу сформулировать как математическую, т. е. описать в математических терминах оба обязательных элемента оптимизации - множество вариантов решений и критерий оптимальности, придавая, таким образом, количественные оценки возможным вариантам и количественную меру их «близости» к цели.
Решение задачи оптимизации первого вида- поиска экстремумов выходасводится к поиску в пределах некоторой области экстремальных значений выхода системы У* - максимума Уmax с координатами Х max и (или) минимума Уmin с координатами Хmin. К решению задачи могут быть привлечены любые методы оптимизации. В том случае, когда поведение системы описывается моделями в виде полиномов не выше второго порядка, целесообразно применять специфический диссоциативно-шаговый метод оптимизации, при котором полином разбивается на n -количество квазиоднофакторных моделей. Они анализируются (вернее их производные) и значения подставляются в общую модель.
В том случае, когда экономико-статистическая модель линейна по факторам, поиск оптимума вне области, как и в области эксперимента, можно вести по одной из модификаций градиентного метода: по методу крутого восхождения Бокса-Уилсона, или по методу наискорейшего спуска. Для того, чтобы от центра эксперимента (Хi =0) перейти в окрестность точки оптимума показателя качества Уopt, необходимо сделать ряд шагов по кратчайшему пути, т.е. по градиенту Δ У. Для реализации такого движения следует изменять факторы Х1…Хк пропорционально соответствующим коэффициентам линейной модели и в ту сторону, куда указывает знак коэффициента. На рисунке 16 изображена последовательность нахождения оптимума по методу крутого восхождения Бокса-Уилсона.
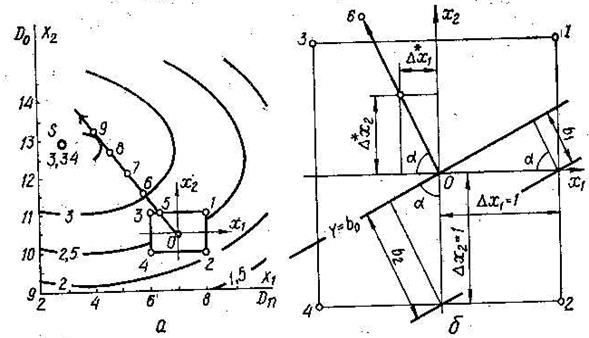
Рисунок 16 – Поиск оптимума по методу Бокса-Уилсона: а – общий выбор точек эксперимента; б – геометрические зависимости при формировании градиента
Решение с помощью полиномиальных моделей задач оптимизации второго вида - минимизация расхода ресурса. В практике анализа, проектирования и управления в области строительного материаловедения и технологии наиболее распространены оптимизационные задачи второго вида, когда необходимо достигнуть заданного уровня функционирования системы Уj тр.= const, израсходовав при этом минимальный ресурс Хj. При решении таких задач возникает ряд трудностей. К числу их относится тот факт, что нелинейное уравнение для определения уровня любого Хi соответствующего Уj тр.= const получается в неявном виде:
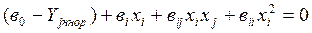 (4.87)
(4.87)
При этом одному значению Уj тр.= const соответствует не одна пара корней, а множество точек на изоповерхности второго порядка в k -мерном пространстве, на котором и нужно найти значение Х, соответствующее минимуму расхода ресурса по одному из факторов. Эти трудности могут быть преодолены с помощью методов нелинейного программирования, а также при применении метода диссоциативно-шаговой оптимизации, направленной на пошаговое уменьшение размерности факторного пространства за счет стабилизации части факторов на оптимальных уровнях Хi opt.
Принятие инженерных решений по комплексу экспериментально-статистических моделей. В материаловедческих и технологических задачах поведение исследуемой системы характеризуется обычно группой критериев качества, координаты оптимума которых, как правило, не совпадают. В силу этого возникает новый круг проблемных вопросов, связанных с принятием компромиссных решений в многокритериальных инженерных задачах. Выбор компромиссного решения не может быть сделан без введения дополнительных правил. Размер группы критериев качества должен быть уменьшен за счет установления корреляционных связей между критериями и исключением тех из них, изменение которых допустимо оценивать по другим оставшимся критериям. Можно построить на основе единичных критериев некоторый интегральный критерий как функцию V=f(Yi …Yj …Y0) и для него искать экстремальные значения. Примером такого интегрального критерия является себестоимость единицы продукции. Можно с помощью квалифицированных экспериментов установить приоритет критериев, проранжировав их как У(j) по степени важности для состояния данной системы в целом. Компромиссная задача решается последовательно путем поиска области, удовлетворяющей требованиям по наиболее важному критерию, затем в этой области определяется подобласть, удовлетворяющая требованиям по второму критерию и т.д. Принцип приоритета весьма плодотворен - он применяется при построении интегральных критериев, в частности критерия желательности.
Для поиска компромиссных решений весьма удобно использовать оптимизацию диссоциативно-шаговым методом. Сначала для каждого из Ө критериев Уэ находятся индивидуальные координаты оптимума Х{Yj} в виде k -мерных векторов. Далее формируется матрица размером k× Ө, в которой Ө критериев размещаются ранжированно по приоритетам. В матрице выбирается и стабилизируется тот фактор Хi, уровни которого Хi*{Yj} для всех или наиболее важных критериев совпадают. Таким образом, размерность факторного пространства сокращается на единицу, а результаты стабилизации фактора на общем уровне Хi общ оцениваются по снижению уровня тех критериев, для которых Хi общ ≠ Хi*{Y}. Если результаты приемлемы для технолога, то процедура повторяется, начиная с поиска (k-1)-ый индивидуальной координаты оптимума.
Этот способ позволяет принимать компромиссные решения очень гибко, оценивая в инженерных терминах результаты каждого шага, и при необходимости возвращаться назад. После того как за R шагов размерность факторного пространства сокращена до k-R≤ 3, принятие компромиссных решений резко упрощается, поскольку появляется возможность графически отобразить любое количество изоповерхностей для Q показателей качества. На последнем этапе применяется комплекс двухфакторных диаграмм, каждая из которых может быть представлена семейством изолиний или таблицами с шагом квантования Δ Хi.
При классификации компромиссных задач по инженерным формулировкам наиболее распространенной оказывается задача о выборе рецептуры и технологических режимов получения материалов с комплексом свойств, отвечающих в общем случае двухсторонним нормативам.
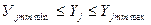 (4.88)
(4.88)
В области сначала должна быть определена разрешенная подобласть Ω тр, а затем в ней точка, удовлетворяющая требованиям экономии ресурсов или наибольшей устойчивости решения и колебаниям процесса.
С помощью группы двухфакторных диаграмм можно решить ещё одну важную инженерную задачу, характерную для практики материаловедческих исследований.
В ряде случаев целесообразно анализировать поведение системы по некоторому j- му показателю качества при условии, что уровень другого её отклика постоянен - Уj= const (без потери общности). Такой анализ назван изопараметрическим. Так, в технологии бетона уровни свойств затвердевшего материала нередко сравниваются между собой при условии постоянства такого косвенного реологического параметра, как подвижность бетонной смеси. Эти смеси называются равноподвижными, а в более общей терминологии - изореологическими. В технологии ячеистых бетонов их механические показатели сравниваются при одинаковой плотности или пористости материала и т.п.
Экспериментальное определение составов и технологии изготовления изопараметрических образцов весьма трудоемко, так как требуются предварительные опыты для достаточно точного попадания на заданный уровень свойства, например, на заданную вязкость смеси. В то же время использование комплекса экспериментально-статистических моделей позволяет решать такие задачи достаточно просто и легко.
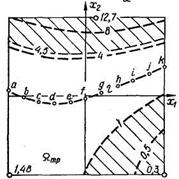
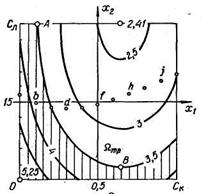
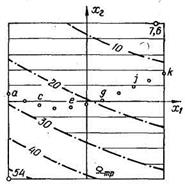
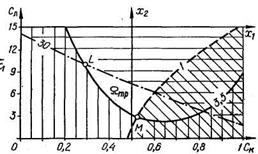
По определению, на любой изолинии двухфакторной диаграммы уровень отклика системы постоянен - Уj = f(x1, x2) = const, а, следовательно, движение вдоль изолинии возможно только тогда, когда каждому изменению фактора x2 соответствует функционально заданное изменение фактора x1 = ψ (x2). Поскольку уровни факторов x1 и x2 вдоль изолинии Уj = const изменяются, то это влечет за собой изменения j –го свойства материала. Анализируя эти изменения, можно получить новую материаловедческую и технологическую информацию. На рисунке 17 представлен порядок оптимизации с помощью группы двухфакторных диаграмм на примере анализа влияния состава композита на время отвердевания композита, модуль упругости и предел прочности. Как видно из рисунка сначала определяют область допустимых значений отдельно по каждому параметру, а затем проводится комплексный анализ сразу по всем трем свойствам.
Вышеизложенные методы решения компромиссных задач на двухфакторных диаграммах могут быть развиты на трехфакторные ситуации, рассматриваемые на объемных диаграммах. Это нередко оказывается необходимым в тех случаях, когда область допустимых решений слишком мала и, целесообразно искать возможности её расширения до заданного значения за счет изменения уровней третьего фактора.
|
|
|
|
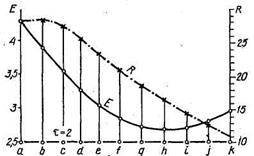 |
Е – модуль упругости, R – предел прочности, τ – время отвердевания композита по двухфакторным моделям; x1 – концентрация кремнеорганической жидкости, x2 – концентрация латекса
Рисунок 17 – Комплексный анализ свойств: а – изолинии Е и область допустимых решений Етр < 3, 5 МПа; б – изолинии R и область Rтр > 30 МПа; в – изолинии τ и область 1< τ < 4, 5 ч; г – допустимая область Утр для всех трех свойств; д – изопараметрический анализ Е и R при τ = 2 = const