
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дисперсионная матрица оценок
|
|
Распишем систему уравнений (4.44) подробнее:
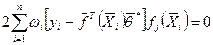 (4.45)
(4.45)
где j = 1, 2, …, m.
Эту систему после преобразования запишем в виде
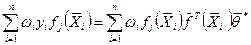 (4.46)
(4.46)
где j = 1, 2, …, m.
Пусть 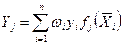 (4.47)
(4.47)
Тогда
 (4.48)
(4.48)
Обозначим
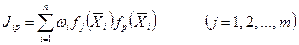 (4.49)
(4.49)
Так что
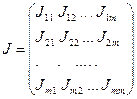 (4.50)
(4.50)
Теперь соотношение (4.46) можно записать в виде
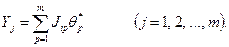 (4.51)
(4.51)
А всю систему запишем так:
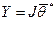 (4.52)
(4.52)
Решение этой системы в матричной форме имеет вид
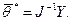 (4.53)
(4.53)
где J - информационная матрица Фишера.
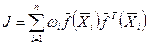 (4.54)
(4.54)
Обратная матрица является дисперсионной матрицей оценок
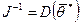 (4.55)
(4.55)
Дисперсионная матрица играет большую роль при выборе наилучших оценок. Оценка 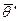 предпочтительнее оценки
предпочтительнее оценки 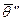 , если дисперсионная матрица
, если дисперсионная матрица 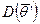 меньше дисперсионной матрицы
меньше дисперсионной матрицы 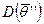 или определитель
или определитель
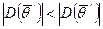 (4.56)
(4.56)
Итак, наилучшие линейные оценки для рассматриваемого эксперимента найдены. Но может быть и другой эксперимент с другим n и другим набором факторов. Следует обратить внимание на то, что наилучшей линейной оценкой поверхности отклика 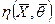 является
является
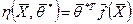 (4.57)
(4.57)
Дисперсия оценки 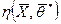 равна
равна 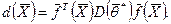 .
.
Критерии оптимального планирования
Следующей проблемой после выбора типа функции η является определение таких численных значений неизвестных параметров θ 1, …, θ т, при которых функция регрессии будет достаточно хорошо (или даже наилучшим образом) описывать эмпирические данные. Для её решения прежде всего необходимо задать критерий, который определял бы степень соответствия эмпирических данных и регрессионной зависимости. Любой такой критерий должен учитывать отклонения между измеренными значениями у1..., yN и приближенными значениями.
Критерии оптимального выбора θ могут быть заданы различными способами. Например, наилучшим могут считаться те θ, для которых величины минимальны.
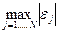 ,
, 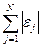 ,
, 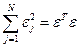 (4.58)
(4.58)
Многие экспериментальные ситуации таковы, что нельзя (по крайней мере без дополнительных экспериментов) задать один критерий оптимальности, но можно указать множество критериев {Фα (ξ)}, каждый из которых желательно минимизировать выбором ξ. При этих условиях задача планирования многокритериальна.
Можно утверждать, что специфической задачей теории планирования эксперимента является конструирование критерия его оптимальности. Второй задачей является экстремальная (может быть очень сложная) задача. Можно выделять некоторые классы экстремальных задач теории планирования эксперимента, допускающих специальные методы исследования, но роль общей теории решения экстремальных задач приуменьшить нельзя. В соответствии с этой точкой зрения основное внимание уделяется критериям оптимальности, их конструированию и их свойствам. При конструировании критерия важную роль играет априорная информация, находящая свое отражение в высказываемой экспериментатором гипотезе модели изучаемого явления.
Эксперимент как активное воздействие на объект с целью получения необходимого эффекта требует на свою реализацию некоторого расхода ресурсов: материальных, временных, трудовых и др. Эксперимент может быть оптимизирован по двум граничным направлениям:
1) если исследователь может израсходовать на эксперимент весь имеющийся в наличии ресурс, то естественно его стремление получить максимально возможный объем новой информации о поведении, структуре, надежности и других сторонах исследуемого объекта;
2) если исследователю задан уровень необходимого эффекта или объем информации о поведении объекта, то естественно его стремление к тому, чтобы достигнуть результата при минимальном расходе ресурсов (уменьшая количество опытных установок и образцов, сокращая сроки работы, не привлекая специалистов определенного уровня и т.п.).
На основании вышеизложенного следуют выводы, определяющие некоторые основные принципы оптимального планирования эксперимента. Во-первых, из системы нормальных уравнений для определения L неизвестных оценок bi в модели, линейной по параметрам, следует, что необходимо и достаточно, чтобы матрица Х содержала L разных строк. Следовательно, минимальное число опытов в плане Nmin = L (насыщенный план), а избыточность опытов N – L полезна не с алгебраической, а со статистической точки зрения. Во-вторых, ковариационная матрица D определяет не только численные значения вектора Β неизвестных оценок коэффициентов модели, но и характеристики точности модели как в целом, так и отдельных ее параметров. Диагональные элементы матрицы cii оценивают дисперсии оценок каждого коэффициента S2{bi}, следовательно, точность оценок будет различной, если эти элементы не равны между собой. Внедиагональные элементы cij определяют корреляцию оценок коэффициентов модели и если ρ {bi bj}≠ 0, то работа исследователя с моделью усложниться. В-третьих, ковариационная матрица D = ХТХ-1 не зависит от результатов эксперимента и, следовательно, может быть исследована до его реализации. Результаты такого анализа могут служить основой для конструирования матрицы плана Х некоторым оптимальным (с точки зрения целей исследования системы) образом до проведения опытов. До опыта можно исследовать и меру точности предсказания выхода d= ХТ Dx, связанную только с расположением опытных точек, использовать результаты анализа для повышения точности модели и т.п.
Исследование матриц D, мер точности d и других статистических характеристик с целью конструирования матриц плана Х и есть одно из направлений оптимального алгоритмизированного планирования эксперимента. Оптимальность оценивается по большому числу критериев, каждый из которых приобретает ту или иную ценность для экспериментатора в зависимости от целей его исследований. Эти критерии в абстрактной математической форме обобщают ту массу пожеланий, которые выдвигают к результатам исследований. Ниже приведены критерии, имеющие наибольшее распространение в материаловедении и технологии и наиболее важны для решения прикладных технико-экономических задач.
Из анализа формул следуют критерии, связанные с определением и минимизацией дисперсии оценок коэффициентов модели:
а) оценки коэффициентов модели будут независимыми только при ρ {bi bj}=0, что приводит к диагональности матрицы [D]. При этом угол поворота Ω =0 и направление главных осей эллипсоида рассеяния (γ и π в линейной однофакторной модели) совпадает с направлением координатных осей пространства параметров, а размеры его большого и малого диаметров могут определяться как индивидуальные доверительные интервалы оценок bi. План, обеспечивающий ρ {bi bj}=0, называется ортогональным (рисунок 12, д). В таком плане суммы по всем N опытам равны 0, а для двухуровневых планов, кроме того, действительно соотношение:

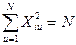 (4.59)
(4.59)
б) для минимизации обобщенной дисперсии, пропорциональной объему эллипсоида рассеяния оценок параметра, а для линейной однофакторной модели – площади эллипса 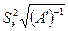 , необходимо минимизировать определитель ковариационной матрицы или максимизировать определитель информационной матрицы [М], в частности
, необходимо минимизировать определитель ковариационной матрицы или максимизировать определитель информационной матрицы [М], в частности 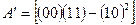 . План, соответствующий требованию mindet [М]-1 на множества планов, отвечает критерию D-оптимальности (determinant) (рисунок 12, а). Этот критерий наиболее тесно связан с центральными идеями математической статистики (с теорией эффективных оценок) и является одним из важнейших в современной математической теории эксперимента. План обеспечивает максимальную величину определителя главной матрицы (информационной) и минимальную величину определителя матрицы дисперсий (это транспонированная информационная матрица);
. План, соответствующий требованию mindet [М]-1 на множества планов, отвечает критерию D-оптимальности (determinant) (рисунок 12, а). Этот критерий наиболее тесно связан с центральными идеями математической статистики (с теорией эффективных оценок) и является одним из важнейших в современной математической теории эксперимента. План обеспечивает максимальную величину определителя главной матрицы (информационной) и минимальную величину определителя матрицы дисперсий (это транспонированная информационная матрица);
в) минимальная средняя дисперсия оценок коэффициентов связана с поиском суммы квадратов длин осей эллипсоидов рассеяния (для эллипса из: 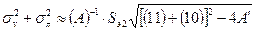 или минимума длины диагонали
или минимума длины диагонали 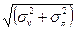 многомерного прямоугольника, описанного вокруг эллипсоида. Для этого минимизируется след матрицы t2[D] (или [(11)+(00)]→ min). Такой критерий носит название А-оптимальность (averadge variance) (рисунок 12, б);
многомерного прямоугольника, описанного вокруг эллипсоида. Для этого минимизируется след матрицы t2[D] (или [(11)+(00)]→ min). Такой критерий носит название А-оптимальность (averadge variance) (рисунок 12, б);
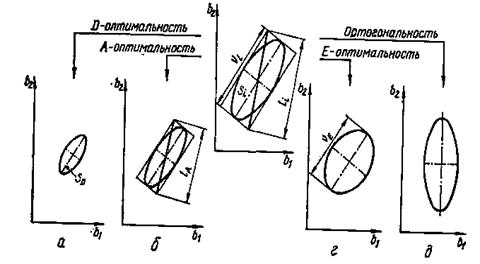
Рисунок 12 – Взаимосвязь критериев оптимальности с эллипсом рассеяния: а – D -оптимальность; б – А -оптимальность; в – параметры эллипса; г – Е -оптимальность; д – ортогональность
г) для минимизации максимальной оси эллипсоида рассеяния (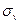 ) минимакс собственного значения (eigen value) матрицы [D] - критерий Е-оптимальности (рисунок 12, г). В этом случае отдельные оценки параметров модели не будут обладать слишком большими дисперсиями и ковариациями.
) минимакс собственного значения (eigen value) матрицы [D] - критерий Е-оптимальности (рисунок 12, г). В этом случае отдельные оценки параметров модели не будут обладать слишком большими дисперсиями и ковариациями.
С оценками коэффициентов модели связаны и такие критерии оптимальности планов, как минимакс дисперсии оценок коэффициентов (minimax cii) и минимум суммы относительных ошибок оценок min 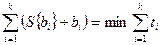 .
.
Из анализа меры точности d следуют критерии, связанные с ошибкой модели в целом:
а) если необходимо обеспечить минимум средней дисперсии оценки выхода или 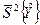 , то должна быть минимальная функция
, то должна быть минимальная функция  , что соответствует критерию Q-оптимальности;
, что соответствует критерию Q-оптимальности;
б) минимуму максимального значения дисперсии оценки min(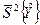 )max соответствует minimax d, а критерий называется G-оптимальность (general variance);
)max соответствует minimax d, а критерий называется G-оптимальность (general variance);
в) постоянство дисперсии предсказания на равных расстояниях от центра эксперимента – ротатабельность – обеспечивается при d=f{ρ }, где ρ = 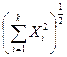 ;
;
г) если в пределах (|ρ |≤ 1), желательно обеспечить постоянство дисперсии предсказания 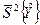 ≈ с onst, униформность, то должно обеспечиваться кроме ротатабельности, и условия d≈ сonst, что достигается повторением опытов, в частности в центре плана.
≈ с onst, униформность, то должно обеспечиваться кроме ротатабельности, и условия d≈ сonst, что достигается повторением опытов, в частности в центре плана.
К числу критериев, облегчающих процедуру экспериментов и построение моделей, можно отнести следующие:
а) минимизация числа опытов, то есть близость числа опытов N к числу оцениваемых параметров модели α. По-видимому, особый интерес этот критерий будет вызывать у экспериментатора на первом поисковом этапе исследования, когда можно получить даже не очень точное представление об объекте, но при минимуме затрат материальных и временных ресурсов;
б) простота вычислений коэффициентов модели;
в) композиционность плана – возможность использовать точки плана первого этапа в плане второго этапа в случае, если модель первого этапа (полином степени m, например, линейный) неадекватно описывает поведение системы (требуется описание полиномом степени m+1, например, квадратичным).
Наличие такого большого числа, часто несовместимых критериев оптимальности, с одной стороны, усложняет принятие решения о выборе плана экспериментатором, с другой стороны, дает ему возможность построить (или выбрать) план в соответствии с целями данного этапа исследований. В настоящее время в результате развития общей методологии математической теории эксперимента теперь нет необходимости выбирать один какой-нибудь критерий, а появилась возможность построения компромиссных планов достаточно хороших с позиций разных критериев [7].
Планы для построения линейных и неполных квадратичных моделей
Линейная модель имеет вид:
Y = B0 + Σ BiXi (4.60)
Для построения таких моделей целесообразно использовать полный факторный двухуровневый план типа 2К, в котором реализуются все возможные сочетания двух уровней факторов «+1» и «-1» (где К – количество факторов). Число возможных сочетаний определяется количеством факторов и составляет N = 2К. В таблице 5 представлены возможные сочетания уровней для двух факторов.
Для двух факторов, которые принимают в опыте по два значения, число сочетаний или опытов равно
N = 22 = 4 (4.61)
Таблица 5 - Полный факторный двухуровневый план типа 2К
| № опыта | Х1 | Х2 |
| +1 | +1 | |
| +1 | -1 | |
| -1 | +1 | |
| -1 | -1 |
Таблица представляет собой матрицу планирования эксперимента: строки матрицы соответствуют различным опытам, а столбцы значениям факторов.
Полный факторный план для всего количества факторов можно построить самостоятельно, переходя от матриц меньшей размерности к матрицам большей размерности путем увеличения числа факторов на единицу. При этом исходный план записывается дважды для каждого уровня нового фактора. Так, для построения плана 23 используется план типа 22 (таблица 6).
Таблица 6 - Полный факторный трехуровневый план типа 2К
| № | Х1 | Х2 | Х3 |
| +1 | +1 | +1 | |
| +1 | -1 | +1 | |
| -1 | +1 | +1 | |
| -1 | -1 | +1 | |
| +1 | +1 | -1 | |
| +1 | -1 | -1 | |
| -1 | +1 | -1 | |
| -1 | -1 | -1 |
Полные факторные эксперименты широко распространены вследствие простоты вычисления коэффициентов регрессии:
B0 = 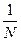
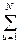 YU (4.62)
YU (4.62)
Β i = 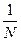
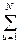 XiuYU (4.63)
XiuYU (4.63)
где N – количество факторов;
YU – результаты эксперимента;
Xi - факторы;
U – строка плана.
Помимо простоты вычислений план обеспечивает получение независимых от Х оценок коэффициентов уравнения. Это значит, что исключение из уравнения любого коэффициента не приводит к изменению величин остальных коэффициентов. Это свойство оказывается полезным в том случае, когда нужно оценить степень влияния факторов на отклик без построения модели. Недостаток – перерасход материалов.
Неполные квадратичные модели. Линейная модель не всегда дает возможность описать с нужной точностью изучаемый процесс. В некоторых случаях дополнение линейного уравнения членами взаимодействия Аij повышает его точность и позволяет получить работоспособную модель вида:
Y = b0 + bixi + bijxixy (4.64)
Уравнение называется неполным квадратичным и может включать в общем случае не только парные взаимодействия, но и взаимодействия более высокого порядка, например, тройные: bijkxixjxk. Полные факторные планы позволяют вычислить все возможные взаимодействия факторов. Минимизация числа опытов достигается за счет дробных реплик типа 2К-Р. Для того, чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь, тогда, значение нового фактора определяется знаками этого столбца.
Планы для построения полиномиальных моделей второго порядка
Полином второго порядка от n переменных имеет вид:
Y = b0 + biXi +biiXi2 + bijXiXj (4.65)
Существует большое количество планов для построения данного вида регрессии, наиболее лучшие из них представлены в «Таблицах планов экспериментов» [30].
Все эти планы, помимо различий в свойствах, можно разделить на две большие группы: симметричные и несимметричные. К первым относятся те, у которых выполняется условие:
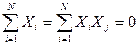 (4.66)
(4.66)
Все остальные называются несимметричными.
Расчет коэффициентов регрессии для симметричных планов осуществляется по ковариационно-корреляционной матрице, которую в общем виде можно представить следующим образом:
 (4.67)
(4.67)
где a*; N*; r*; a-1; p-1; p* - элементы матрицы.
Коэффициенты регрессии находят по упрощенной схеме:
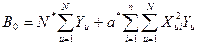
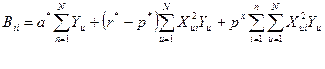 (4.68)
(4.68)
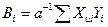
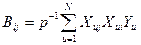
Коэффициенты регрессии несимметричных планов находят по матрице для расчета м.н.к.-оценок параметров моделей, которая в общем виде выглядит следующим образом и обозначается L (таблица 7).
Таблица 7 - Матрица для расчета м.н.к. - оценок параметров моделей
| Θ 0 Θ ii Θ jj Θ i Θ j Θ ij Θ kl | |
| Θ 0 Θ ii Θ jj Θ i Θ j Θ ij | Θ i0 Θ 0ii Θ 0jj Θ 0i Θ 0j Θ 0ij Θ 0kl Θ ii0 Θ iiii Θ iijj Θ iii Θ iij Θ iiij Θ iikl … … … … … … … |
Коэффициенты регрессии вычисляются по формуле:
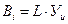 (4.69)
(4.69)
Это означает, что оценку каждого параметра получают как скалярное произведение соответствующей строки матрицы L на вектор наблюдений У, который в общем виде может быть представлен следующим образом (таблица 8):
Таблица 8 – План и результаты эксперимента
| № опыта | Факторы | У | |
| Х1 | Х2 | ||
| +1 | -1 | У1 | |
| -1 | У2 | ||
| ... | … | … | … |
| n | +1 | Уn |
Тогда, например, свободный коэффициент регрессии будет вычисляться следующим образом:
В0=Ө 00У1+ Ө 0iiУ2+ Ө 0jjУ3+ Ө 0iУ4+ Ө 0jУ5+ Ө ijУ6+ Ө 0кеУ7+…+ Ө 0кеУn (4.70)
Квадратичный коэффициент:
Вii= Ө ii0У1+ Ө iiiiУ2+ Ө iijjУ3+ Ө iiiУ4+ Ө iijУ5+ Ө iiijУ6+…+ Ө iiкеУn (4.71)